Bellman Ford
벨만 포드 알고리즘은 음의 가중치가 있는 그래프에서 특정 시작 정점으로부터 다른 모든 노드까지의 최단거리(최소 비용)을 구하고 음의 사이클을 감지할 수 있는 최단 거리 알고리즘입니다.
- 시작 정점에서 다른 모든 노드까지의 최단 경로를 구한다는 점에서 다익스트라와 유사하지만, 벨만 포드는
음수 간선을 처리할 수 있고,음의 사이클도 감지할 수 있다는 차이점이 있습니다. - 유향 그래프를 기반으로 동작하지만, 무향 그래프도 각 간선을 양방향 유향 간선으로 변환하면 적용할 수 있습니다.
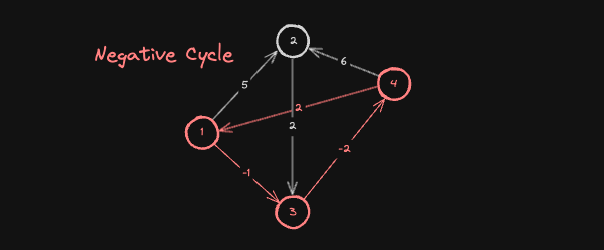
음의 사이클(Negative Cycle)
음의 순환이라고도 하며, 사이클을 구성하는 간선들의 가중치의 합이 0보다 작은 순환 경로를 의미합니다. 즉, 어떤 노드에서 출발하여 여러 간선을 따라 다시 그 노드로 돌아오는 사이클이 있을 때 그 사이클에 포함된 간선들의 가중치 총합이 음수라면 이를 음의 사이클이라고 합니다.
Mechanism
다익스트라는 매 단계마다 가장 가까운 노드를 찾아 그 노드의 최단 거리를 확정해 나가는 방식이라면, 벨만포드는 모든 간선을 확인하며 출발 노드로부터 다른 노드들까지의 최단 거리의 상한값을 점진적으로 줄여 나가는 완화(Relaxation) 과정을
노드의 개수 - 1번 반복함으로써 최종적인 최단 거리를 찾아내는 방식으로 동작합니다. 이 과정을 통해, 출발 노드로부터 모든 노드까지의 최단 거리 정보를 정확하게 계산할 수 있습니다. 보다 구체적인 동작 과정은 다음과 같습니다.
- 시작 노드를 설정한 다음, 시작 노드의 최단 거리는
0, 나머지 모든 노드는무한대(INF)로 초기화합니다. - 노드의 개수
N - 1만큼 다음 과정을 반복합니다.- 모든 간선
E를 하나씩 확인하면서,현재 노드를 거쳐 도착 노드로 가는 비용이 더 작으면 최단 거리 테이블을 갱신합니다.
- 모든 간선
- 2번 과정을 한 번 더 수행하여 음수 간선 순환이 발생하는지 검증합니다. 이때, 최단 거리 테이블이 갱신된다면 음수 간선 순환이 존재하는 것입니다.
INF라는 값은 아직 출발 노드로부터 해당 노드에 도달한 적이 없다는 것을 말합니다.
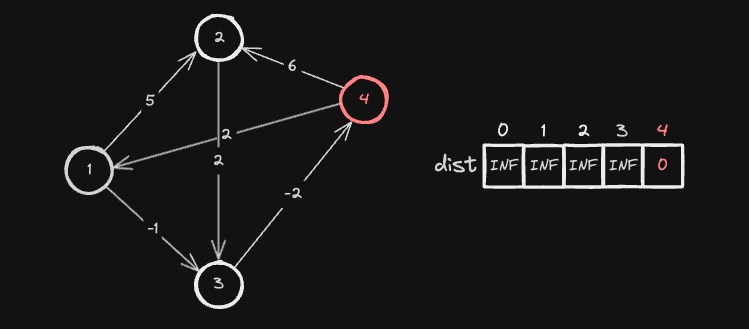
Initialize
가장 먼저 시작 노드를 설정합니다. 그리고 시작 노드의 최단 거리를 0으로 갱신하고, 나머지 모든 노드는 무한대(INF)로 초기화합니다. 아래 예제에서의 출발 노드는 4입니다.
Iterate Relaxation
이제 모든 간선들을 확인하면서 각 간선을 거쳐 다른 노드로 이동했을 때 더 짧은 경로가 발견되면, 해당 노드의 최단 거리 상한을 줄여나가는 완화 작업을 노드의 개수 N - 1번 만큼 반복합니다.
Relaxation 1
1번 Node ── cost ──▶ 2번 Node 간선을 따라 이동했을 때, 2번 노드까지의 기존 최단 거리보다 1번 노드의 최단 거리 + 간선 가중치가 더 작다면, 2번 노드의 최단 거리를 갱신합니다.
- 즉,
dist[2] > dist[1] + cost라면dist[2] = dist[1] + cost로 갱신합니다. - 1번 노드는 아직 출발 노드로부터 도달한 적 없기 때문에 비교할 수 없습니다. 따라서
dist[2]의 최단 거리를 갱신하지 않습니다.

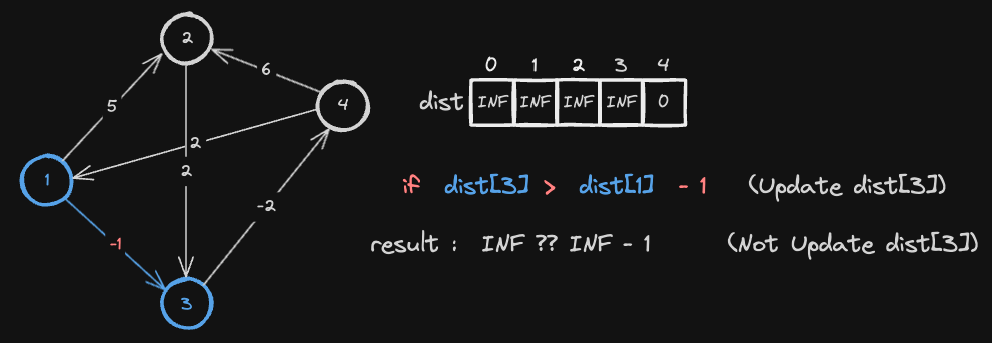
1번 Node ── cost ──▶ 3번 Node 간선을 따라 이동했을 때, 3번 노드까지의 기존 최단 거리보다 1번 노드의 최단 거리 + 간선 가중치가 더 작다면, 3번 노드의 최단 거리를 갱신합니다.
- 즉,
dist[3] > dist[1] + cost라면dist[3] = dist[1] + cost로 갱신합니다. - 1번 노드는 아직 출발 노드로부터 도달한 적 없기 때문에 비교할 수 없습니다. 따라서
dist[3]의 최단 거리를 갱신하지 않습니다.
2번 Node ── cost ──▶ 3번 Node 간선을 따라 이동했을 때, 3번 노드까지의 기존 최단 거리보다 2번 노드의 최단 거리 + 간선 가중치가 더 작다면, 3번 노드의 최단 거리를 갱신합니다.
- 즉,
dist[3] > dist[2] + cost라면dist[3] = dist[2] + cost로 갱신합니다. - 2번 노드는 아직 출발 노드로부터 도달한 적 없기 때문에 비교할 수 없습니다. 따라서
dist[3]의 최단 거리를 갱신하지 않습니다.

3번 Node ── cost ──▶ 4번 Node 간선을 따라 이동했을 때, 4번 노드까지의 기존 최단 거리보다 3번 노드의 최단 거리 + 간선 가중치가 더 작다면, 4번 노드의 최단 거리를 갱신합니다.
- 즉,
dist[4] > dist[3] + cost라면dist[4] = dist[3] + cost로 갱신합니다. - 3번 노드는 아직 출발 노드로부터 도달한 적 없기 때문에 비교할 수 없습니다. 따라서
dist[4]의 최단 거리를 갱신하지 않습니다.

4번 Node ── cost ──▶ 1번 Node 간선을 따라 이동했을 때, 1번 노드까지의 기존 최단 거리보다 4번 노드의 최단 거리 + 간선 가중치가 더 작다면, 1번 노드의 최단 거리를 갱신합니다.
- 즉,
dist[1] > dist[4] + cost라면dist[1] = dist[4] + cost로 갱신합니다. - 4번 노드는 시작 노드이기 때문에 이미 최단 거리 테이블이 갱신되어 있습니다. 따라서 최단 거리를 비교할 수 있습니다. 비교 구문이 INF > 2 참이기 때문에
dist[1]의 최단 거리를 2로 갱신합니다.

4번 Node ── cost ──▶ 2번 Node 간선을 따라 이동했을 때, 2번 노드까지의 기존 최단 거리보다 4번 노드의 최단 거리 + 간선 가중치가 더 작다면, 2번 노드의 최단 거리를 갱신합니다.
- 즉,
dist[2] > dist[4] + cost라면dist[2] = dist[4] + cost로 갱신합니다. - 4번 노드는 시작 노드이기 때문에 이미 최단 거리 테이블이 갱신되어 있습니다. 따라서 최단 거리를 비교할 수 있습니다. 비교 구문이 INF > 6 참이기 때문에
dist[2]의 최단 거리를 6으로 갱신합니다.

이렇게 모든 간선을 한 번씩 확인하고 최단 거리 상한을 갱신하는 첫 번째 완화 작업이 끝났습니다. 완화 전 & 후 최단 거리 테이블을 비교하면 다음과 같습니다.
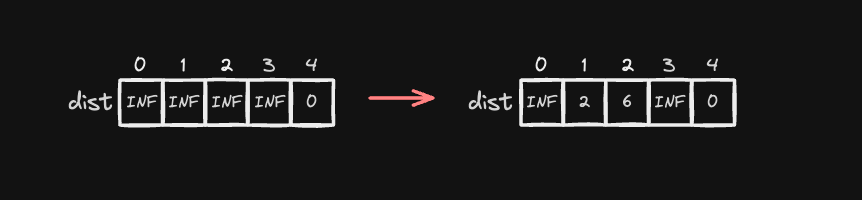
이 과정을 노드의 총 개수 N - 1번 반복하므로, 앞으로 N - 2번 더 반복하면 됩니다. 총 반복 횟수 4 - 1 = 3에서 한 번 작업을 수행했으니 2번만 더 반복하면 됩니다.
Relaxation 2
1번 Node ── cost ──▶ 2번 Node 간선을 따라 이동했을 때, 2번 노드까지의 기존 최단 거리보다 1번 노드의 최단 거리 + 간선 가중치가 더 작다면, 2번 노드의 최단 거리를 갱신합니다.
- 즉,
dist[2] > dist[1] + cost라면dist[2] = dist[1] + cost로 갱신합니다. - 비교 구문이 6 > 7 거짓이기 때문에,
dist[2]의 최단 거리를 갱신하지 않습니다.

1번 Node ── cost ──▶ 3번 Node 간선을 따라 이동했을 때, 3번 노드까지의 기존 최단 거리보다 1번 노드의 최단 거리 + 간선 가중치가 더 작다면, 3번 노드의 최단 거리를 갱신합니다.
- 즉,
dist[3] > dist[1] + cost라면dist[3] = dist[1] + cost로 갱신합니다. - 비교 구문이 INF > 1 참이기 때문에,
dist[3]의 최단 거리를 1로 갱신합니다.

2번 Node ── cost ──▶ 3번 Node 간선을 따라 이동했을 때, 3번 노드까지의 기존 최단 거리보다 2번 노드의 최단 거리 + 간선 가중치가 더 작다면, 3번 노드의 최단 거리를 갱신합니다.
- 즉,
dist[3] > dist[2] + cost라면dist[3] = dist[2] + cost로 갱신합니다. - 비교 구문이 1 > 8 거짓이기 때문에,
dist[3]의 최단 거리를 갱신하지 않습니다.

3번 Node ── cost ──▶ 4번 Node 간선을 따라 이동했을 때, 4번 노드까지의 기존 최단 거리보다 3번 노드의 최단 거리 + 간선 가중치가 더 작다면, 4번 노드의 최단 거리를 갱신합니다.
- 즉,
dist[4] > dist[3] + cost라면dist[4] = dist[3] + cost로 갱신합니다. - 비교 구문이 0 > -1 참이기 때문에,
dist[4]의 최단 거리를 -1로 갱신합니다.

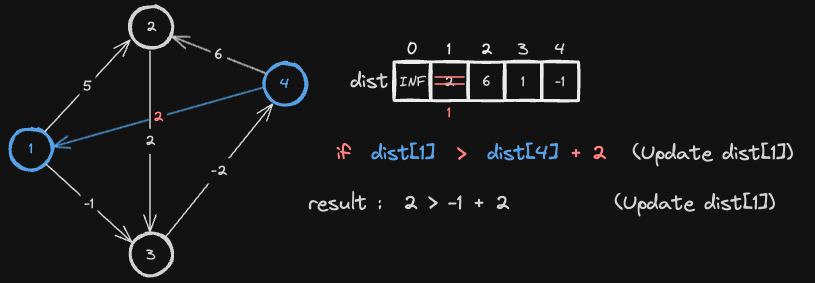
4번 Node ── cost ──▶ 1번 Node 간선을 따라 이동했을 때, 1번 노드까지의 기존 최단 거리보다 4번 노드의 최단 거리 + 간선 가중치가 더 작다면, 1번 노드의 최단 거리를 갱신합니다.
- 즉,
dist[1] > dist[4] + cost라면dist[1] = dist[4] + cost로 갱신합니다. - 비교 구문이 2 > 1 참이기 때문에
dist[1]의 최단 거리를 1로 갱신합니다.
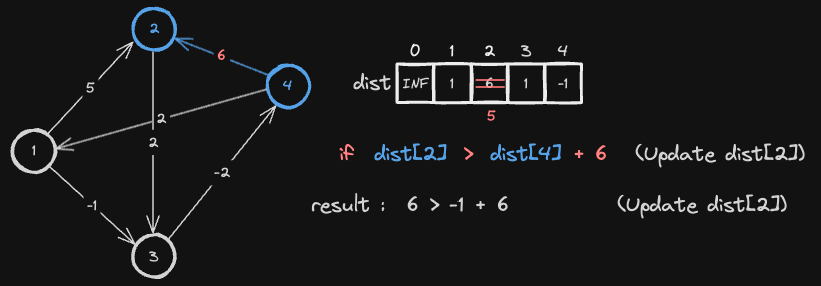
4번 Node ── cost ──▶ 2번 Node 간선을 따라 이동했을 때, 2번 노드까지의 기존 최단 거리보다 4번 노드의 최단 거리 + 간선 가중치가 더 작다면, 2번 노드의 최단 거리를 갱신합니다.
- 즉,
dist[2] > dist[4] + cost라면dist[2] = dist[4] + cost로 갱신합니다. - 비교 구문이 6 > 5 참이기 때문에
dist[2]의 최단 거리를 5로 갱신합니다.
이렇게 모든 간선을 한 번씩 확인하고 최단 거리를 갱신하는 두 번째 Relaxation 단계가 끝났습니다. Relaxation 전후 최단 거리 배열을 비교하면 다음과 같습니다.

이제 마지막 한 번만 더 위 과정을 반복하면 됩니다.
Relaxation 3
너무 중복된 내용이니 생략하고 세 번째 간선 완화 작업 후, 갱신된 최단 거리 테이블만 명시하겠습니다.

Check Negative Cycle
N - 1번의 간선 완화 작업을 모두 수행하면, 시작 노드(4번)로부터 다른 모든 노드까지의 최단 거리가 확정됩니다. 만약 간선 완화 작업을 한 번 더 수행했을 때, 최단 거리가 갱신되는 노드가 있다면 이는 음의 사이클(Negative Cycle)이 존재한다는 것을 의미합니다. 다시 말해
- 음의 사이클에 연결된 노드들로 향하는 간선이 하나라도 존재하거나, 음의 사이클에 속한 노드로부터 도달 가능한 노드가 있다면, 해당 노드들 역시 최단 거리 갱신의 영향을 받아 무한히 작아질 수 있으므로, 결국 최단 경로라는 개념 자체가 성립하지 않게 됩니다.
아래 그래프에서는 1 → 3 → 4 → 1로 이어지는 간선들의 가중치 합이 음수이므로, 음의 사이클이 존재합니다. 또한, 음의 사이클에서 2번 노드로 가는 간선이 존재하기 때문에, 2번 노드 역시 무한히 최단 거리가 작아지는 영향을 받아, 최단 경로라는 개념이 무의미해집니다.
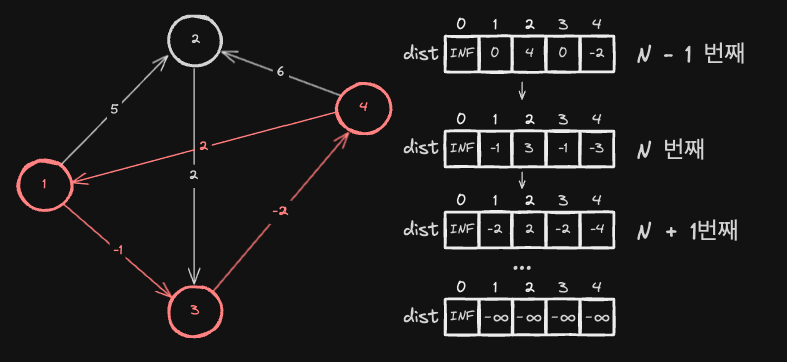
N - 1 번 반복하는 이유
모든 간선을 확인하며 최단 거리 테이블을 갱신하는 간선 완화(Relaxation) 작업을 노드의 개수 - 1번 수행하는 이유는 N개의 노드로 이루어진 사이클이 없는 그래프에서 출발 노드로부터 다른 모든 노드까지의 최단 경로는 아무리 길어도 최대 N - 1개의 간선으로만 구성되기 때문입니다. 최단 경로라면 동일한 같은 정점을 두 번 지날 리 없기 때문이지요. 만약 동일한 정점을 두 번 지나면 순환이 있다는 거구요.
벨만포드는 한 번의 간선 완화(Relaxation) 작업마다 출발 노드로부터 다른 모든 노드들까지의 최단 거리 상한을 줄이면서 갱신해나가기 때문에, N - 1번의 간선 완화 작업이 모두 끝나야 출발 노드로부터 다른 모든 노드들까지의 최단 거리를 확정할 수 있습니다.
하위 모든 그림의 시작 노드는 1입니다.
또한, 그래프에 사이클이 있더라도 모든 최단 경로는 음의 사이클만 포함하지 않는다면, N - 1번의 간선 완화로 출발 노드로부터 다른 모든 노드까지의 최단 거리를 구할 수 있습니다.
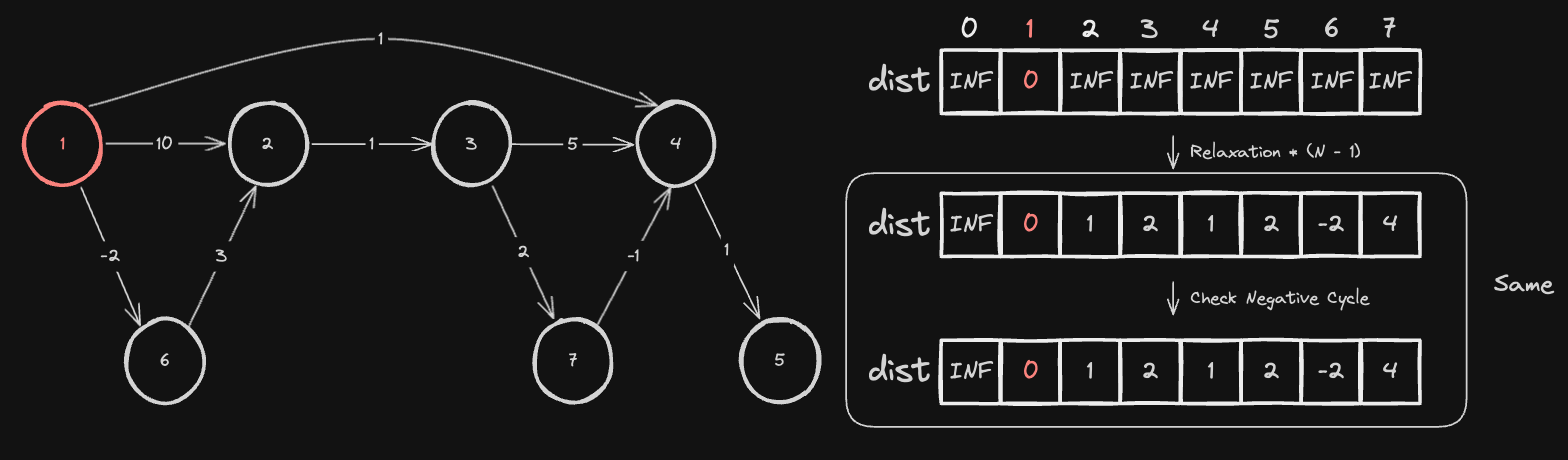
만약 그래프에 음의 사이클이 존재한다면 음의 사이클에 속한 노드로 들어오거나 나갈 수 있는 노드들의 최단 거리가 계속 작아져 결국 음의 발산으로 가기 때문에 최단 거리라는 개념 자체가 성립하지 않게 됩니다.
N - 1번의 간선 완화 작업 후 한 번 더 수행했을 때, 특정 노드에 대한 최단 거리 테이블이 갱신된다면, 이는 음의 사이클이 존재한다는 증거가 됩니다.
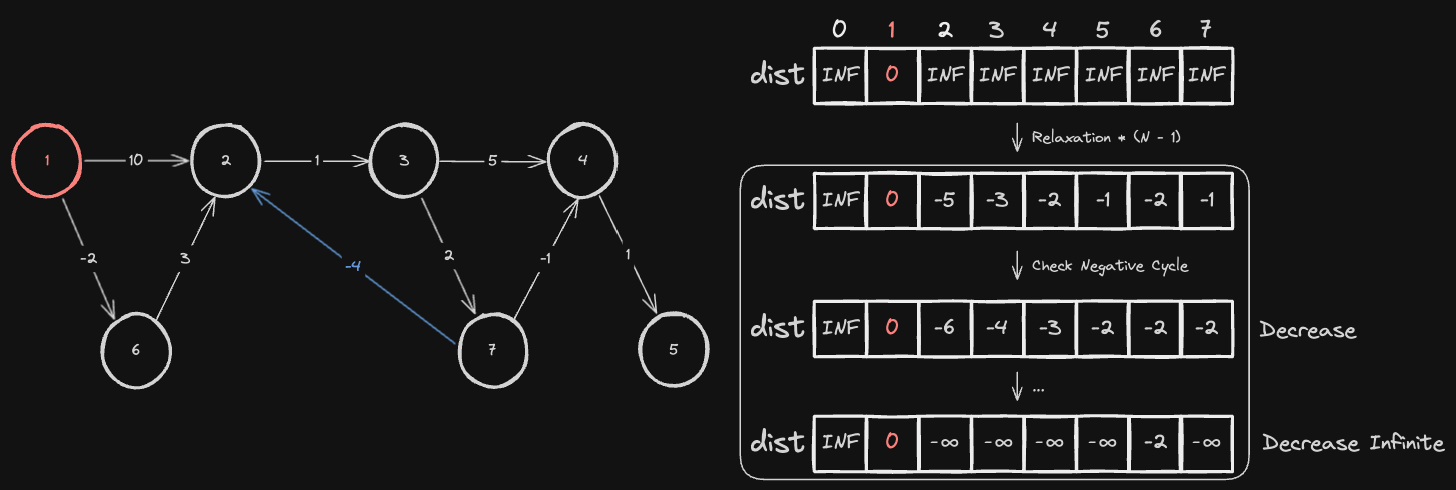
N - 1 번 수행하지 않으면?
간선 완화 작업을 N - 1번 반복하지 않고 그 이하로만 수행할 경우, 간선들의 순서에 따라 최단 거리가 정확하게 계산되지 않을 수 있습니다. 즉, 간선들의 순서가 최적화되어 있지 않다면 최단 거리 갱신이 제대로 이루어지지 않아 올바른 결과를 얻지 못할 위험이 있습니다.
최적의 간선 순서
최적화된 간선 순서란, 그래프 내 최단 경로에 포함된 간선들이 거리 순서대로 배열되어 있거나, 최단 경로를 구성하는 간선들이 반복 작업 초반에 배치되어 있어서, 한 번의 간선 완화 작업만으로 출발 노드에서 모든 노드까지 최단 거리 정보가 정확히 전파되는 경우를 의미합니다.
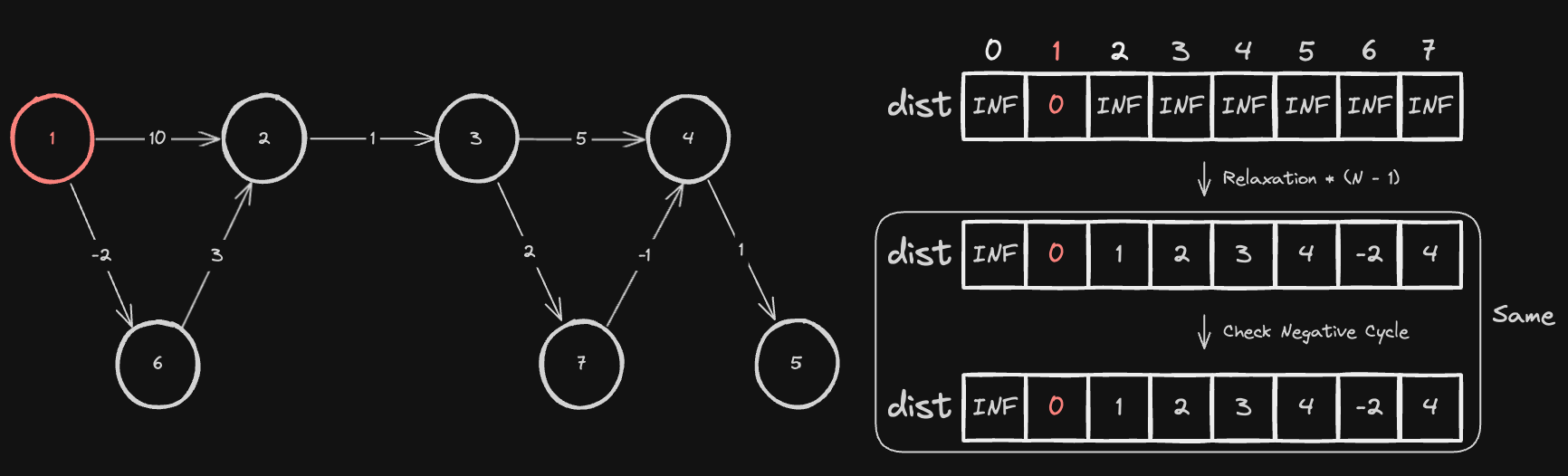
아래 예시처럼 운이 좋게도 주어지는 간선들의 순서가 최적으로 주어진다면, 단 한 번의 간선 완화 작업으로 출발 노드로부터 다른 모든 노드까지의 최단 거리를 구할 수 있습니다.
간선 완화 작업을 1번 했을 때와 N - 1번 수행했을 때 결과가 동일한 것을 볼 수 있습니다.
# (from - cost -> to) 형태
[1, 2, 10], [1, 6, -2], [6, 2, 3], [2, 3, 1], [3, 4, 5],
[3, 7, 2], [7, 4, -1], [1, 4, 1], [4, 5, 1],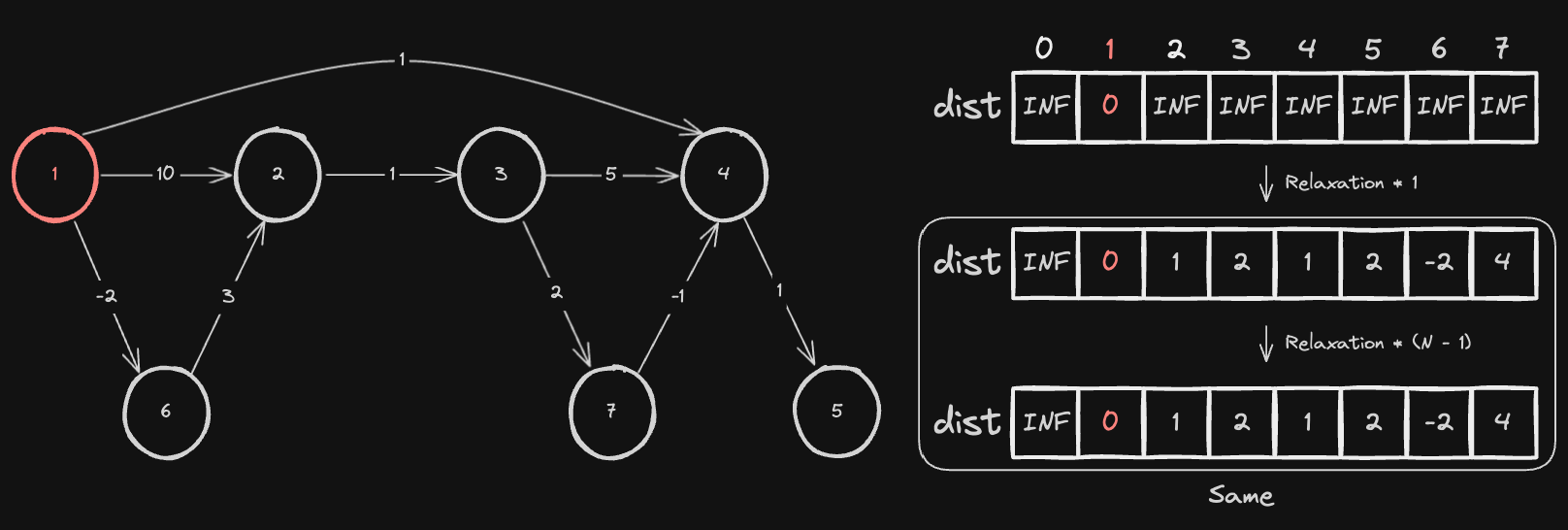
하지만, 주어지는 간선들의 순서를 꼬면, 한 번의 간선 완화 작업으로 출발 노드로부터 다른 모드 노드까지의 최단 거리를 구할 수 없게 됩니다.
간선 완화 작업을 1번 했을 때와 N - 1번 수행했을 때 결과가 다른 것을 볼 수 있습니다.
# (from - cost -> to) 형태
[7, 4, -1], [6, 2, 3], [2, 3, 1], [3, 4, 5], [3, 7, 2],
[1, 4, 1], [4, 5, 1], [1, 2, 10], [1, 6, -2]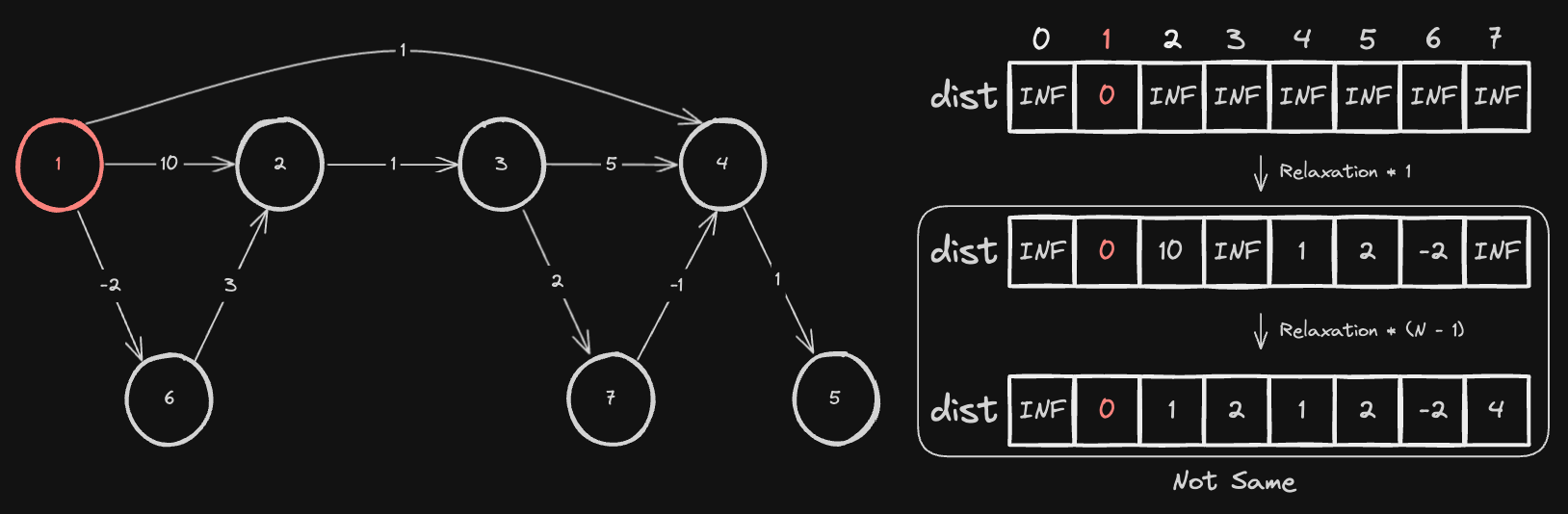
Implementation
벨만 포드 알고리즘은 아래 파이썬 코드로 구현할 수 있습니다.
INF 값에 따른 비교를 주의해야 합니다.
INF를 1e9와 같이 값을 비교할 수 있는 수로 지정했다면, 조건문에
dist[v] != INF and를 꼭 추가해야 합니다. 출발 노드로부터 도달한 적 없는 노드에 대해 값을 갱신하면 안 되기 때문입니다.
def solution(N, edges):
def bellman(st):
dist[st] = 0
for _ in range(N - 1): # Iterate N - 1
for v, nv, cost in edges: # Relaxation
if dist[nv] > dist[v] + cost:
dist[nv], trace[nv] = dist[v] + cost, v # Update Short Distance
for v, nv, cost in edges: # Check Negative Cycle
if dist[nv] > dist[v] + cost:
return True
return False
dist, trace = [float('inf')] * (N + 1), [None] * (N + 1)
st = 1 # Start Node
return ([-1], [], 'Negative Cycle (O)') if bellman(st) else (dist, trace, 'Negative Cycle (X)')
print(solution(7, [[1, 2, 10], [1, 6, -2], [6, 2, 3], [2, 3, 1], [3, 4, 5], [3, 7, 2], [7, 4, -1], [1, 4, 1], [4, 5, 1]])) # Non Negative Cycle Input
print(solution(7, [[1, 2, 10], [1, 6, -2], [6, 2, 3], [2, 3, 1], [3, 4, 5], [3, 7, 2], [7, 4, -1], [4, 5, 1], [7, 2, -4]])) # Negative Cycle Input
# ([inf, 0, 1, 2, 1, 2, -2, 4], [None, None, 6, 2, 1, 4, 1, 3], 'Negative Cycle (X)')
# ([-1], [], 'Negative Cycle (O)')