REVI1337

Dijkstra

12 min read

Dijkstra

다익스트라 알고리즘은 양의 가중치가 있는 그래프의 특정 시작 정점 으로부터 다른 모든 노드로까지의 최소비용 을 구하는 알고리즘입니다.

최소비용은 정점과 정점으로 이어진 간선에 가중치가 주어졌을 때 가중치의 합이 최소가 되는 것을 의미합니다.

Mechanism

다익스트라 알고리즘은 Greedy와 Dynamic Programming이 결합된 알고리즘입니다. 다익스트라의 기본적인 아이디어는 "최단 거리는 최단 거리로 이루어져 있다"는 것에 초점을 둡니다. 즉 최단 거리를 이어 붙여서 또 다른 최단 거리를 만든다는 것입니다. 이 아이디어를 바탕으로 다익스트라는 매 단계마다 가장 가까운 노드를 찾아 그 노드의 최단 거리를 확정해 나가는 방식으로 동작합니다.

  1. 초기화 (각 Node 들의 초기 최소 비용)
  2. 방문 (방문하지 않은 Node 중 가장 비용이 적은 Node 를 선택하여 방문 = Greedy)
  3. 갱신 (방문한 Node 로부터 갈 수 있는 Node 들의 최소비용을 갱신 = Dynamic Programming)

방문한 노드는 다시 탐색하지 않는다.

다익스트라는 한번 방문한 Node 는 다시 탐색하지 않습니다.

아래의 그래프가 있을 때 시작 Node 인 A 로부터 다른 모든 Node 까지의 최소비용을 구하는 예제를 알아보겠습니다.

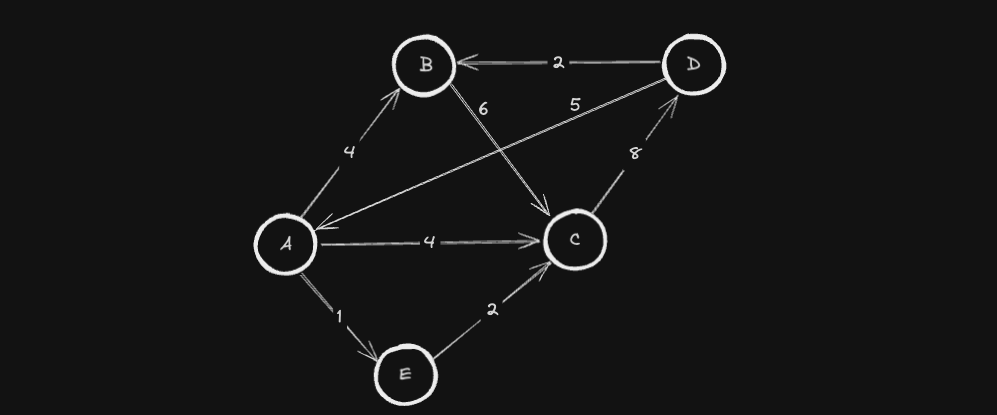
Initialize

  1. 시작 Node 로부터 특정 Node 까지의 최소 비용을 저장할 공간을 생성합니다.
    • 이 때 초기값은 매우 큰 수(예를 들어 INF)로 초기화시킵니다.
  2. 시작 Node 인 A 의 최소비용을 0 으로 갱신시킵니다.
    • 초기화 단계에서는 가장 비용이 적은 Node 를 선택하는 기준이 없기 때문에 시작 Node 인 A 의 비용을 0 으로 갱신하는 것입니다.

Visit & Update

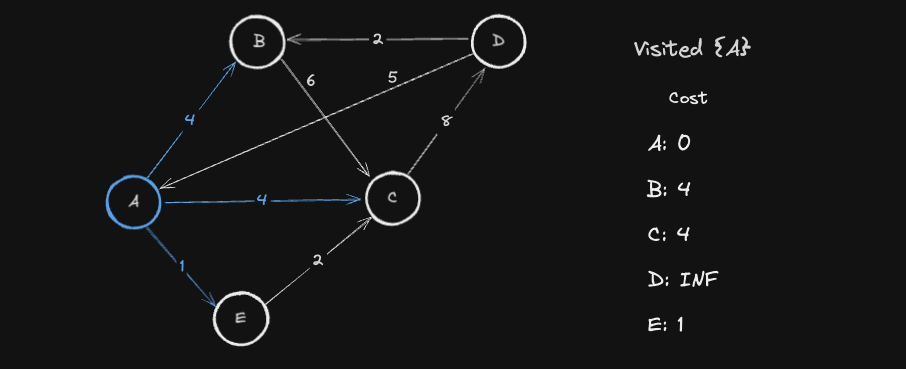
위의 상태에서 방문하지 않은 Node 들 중 가장 비용이 작은 A 를 선택하여 방문합니다. 그리고 A 를 거쳐갈 수 있는 Node 의 비용과 cost 테이블 값과 비교하여 최소비용을 갱신합니다.

  • B 의 경우, A --> B 까지의 비용 (cost[A] + A -> B 간선의 가중치) = 0 + 4 = 4 이 cost 테이블의 노드 B 의 최소비용 INF 보다 작기 때문에 값을 4 로 갱신합니다.
  • C 의 경우, A --> C 까지의 비용 (cost[A] + A -> C 간선의 가중치) = 0 + 4 = 4 이 cost 테이블의 노드 C 의 최소비용 INF 보다 작기 때문에 값을 4 로 갱신합니다.
  • E 의 경우, A --> E 까지의 비용 (cost[A] + A -> E 간선의 가중치) = 0 + 1 = 1 이 cost 테이블의 노드 E 의 최소비용 INF 보다 작기 때문에 값을 1 로 갱신합니다.

이렇게 갱신된 최소비용들은 우선순위 큐에 추가되어 다음 탐색 순서에 반영됩니다.

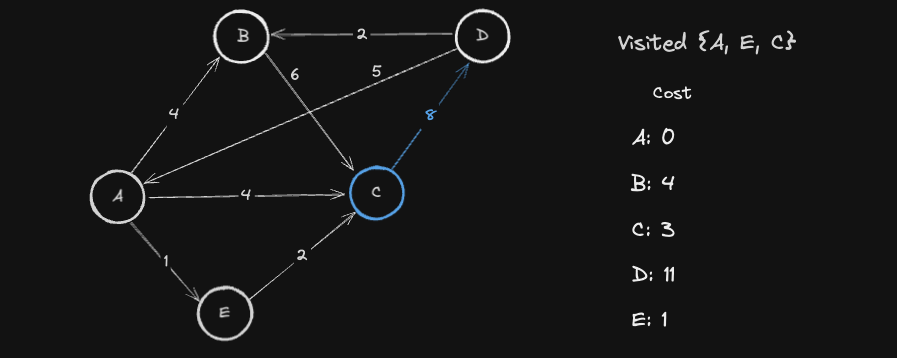
위 상태에서 방문하지 않은 Node 들 중 최소비용인 노드 E 를 선택하여 방문합니다. 그리고 E 를 거쳐갈 수 있는 인접 노드들의 최소 비용을 갱신합니다.

  • C 의 경우, E --> C 까지의 비용 (cost[E] + E -> C 간선의 가중치) = 1 + 2 = 3 이 기존 cost 테이블의 노드 C 의 최소비용 4 보다 작기 때문에 값을 3 로 갱신합니다.

위 상태에서 방문하지 않은 Node 들 중 최소비용인 노드 C 를 선택하여 방문합니다. 그리고 C 를 거쳐갈 수 있는 인접 노드들의 최소 비용을 갱신합니다.

  • D 의 경우, C --> D 까지의 비용 (cost[C] + C -> D 간선의 가중치) = 3 + 8 = 11 이 기존 cost 테이블의 노드 D 의 최소비용 INF 보다 작기 때문에 값을 11 로 갱신합니다.

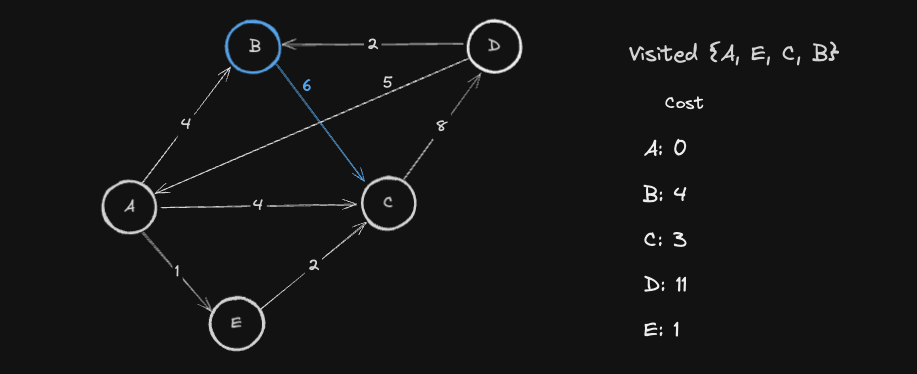
위 상태에서 방문하지 않은 Node 들 중 최소비용인 노드 B 를 선택하여 방문합니다. 그리고 B 를 거쳐갈 수 있는 인접 노드들의 최소 비용을 갱신합니다.

  • C 의 경우, B --> C 까지의 비용 (cost[B] + B -> C 간선의 가중치) = 4 + 6 = 10 이 기존 cost 테이블의 노드 C 의 최소비용 3 보다 크기 때문에 최소비용을 갱신시키지 않습니다.

위 상태에서 방문하지 않은 Node 들 중 최소비용인 노드 D 를 선택하여 방문합니다. 그리고 D 를 거쳐갈 수 있는 인접 노드들의 최소 비용을 갱신합니다.

  • B 의 경우, D --> B 까지의 비용 (cost[D] + D -> B 간선의 가중치) = 11 + 2 = 13 이 기존 cost 테이블의 노드 B 의 최소비용 4 보다 크기 때문에 최소비용을 갱신시키지 않습니다.
  • A 의 경우, D --> A 까지의 비용 (cost[D] + D -> A 간선의 가중치) = 11 + 5 = 16 이 기존 cost 테이블의 노드 A 의 최소비용 0 보다 크기 때문에 최소비용을 갱신시키지 않습니다.

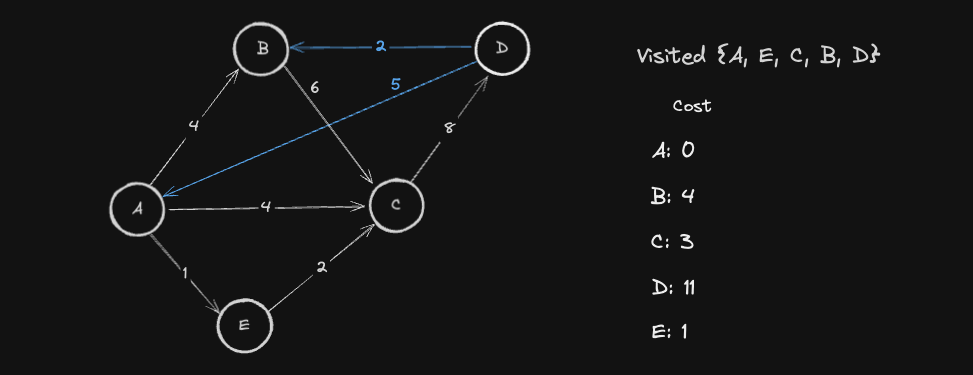
이제 모든 Node 의 방문이 끝났기 때문에 다익스트라가 종료됩니다. 시작 노드 A 로부터 다른 모든 노드로까지의 최소비용 은 위 결과와 같게 됩니다.

노드의 갱신은 아직 방문하지 않은 노드들에 대해서만 이루어지고 있다.

그림을 자세히 보면, 선택된 노드는 다익스트라 알고리즘이 모든 노드를 방문할 때까지(알고리즘이 종료될 때 까지) 최소 비용의 갱신이 더 이상 이루어지지 않았다는 점을 알 수 있습니다.

Implementation

파이썬으로 다익스트라 알고리즘을 구현할 수 있습니다.

4 ~ 7 라인

  • 시작 Node 로부터 특정 Node 까지의 최소 비용을 저장할 공간을 생성합니다. 이때 값은 무한히 큰 값으로 초기화시킵니다.
  • 시작 노드 A 선택 및 방문하여 cost 테이블에 최소비용을 0 으로 갱신합니다.
  • 갱신한 노드의 최소비용과 그 노드를 우선순위 큐 (Priority Queue) 에 [시작노드의 최소비용, 시작노드] 형태로 넣어줍니다.

10 라인

  • 우선순위 큐에서 최소힙 (여기서는 최소비용) 이 되는 값을 pop 합니다. (Greedy)

11 라인

  • 이미 방문한 Node 인지 아닌지 판단하는 조건문이며, 이미 방문한 노드를 재방문하지 않도록 방지하는 로직입니다.
  • pop 한 노드의 비용이 현재 costs 배열에 기록된 내용보다 크다면 이미 방문한 노드로 판단하게 됩니다.
  • 우선순위 큐에서 pop 된 노드는, 전에 해당 노드까지의 최소비용을 이미 갱신했다는 의미입니다. 즉, 현재 pop 한 노드를 기준으로 하는 경로는 이미 이전에 더 짧은 경로가 발견되어 costs 배열에 반영되었기 때문에, 더 큰 비용으로 다시 방문할 필요가 없습니다. 그래서 해당 조건을 통해 이미 더 짧은 경로로 방문된 노드는 무시하고 넘어가도록 하여 불필요한 연산을 줄인 것입니다.
import heapq  
  
def dijkstra(graph, start):  
	pq = []  
    costs = {node: 1e9 for node in graph}  
    costs[start] = 0  
    heapq.heappush(pq, [costs[start], start])  
  
    while pq:  
        cost, vertext = heapq.heappop(pq)   
		if costs[vertext] < cost:         # 이미 방문한 노드면 스킵
            continue  
        for next_vertext, next_cost in graph[vertext].items():  
            total_cost = cost + next_cost  
            if total_cost < costs[next_vertext]:  
                costs[next_vertext] = total_cost  
                heapq.heappush(pq, [total_cost, next_vertext])  
  
    return costs  
  
print(  
    dijkstra(  
        {            
	        'A': {'B': 4, 'C': 4, 'E': 1},  
            'B': {'C': 6},  
            'C': {'D': 8},  
            'D': {'B': 2, 'A': 5},  
            'E': {'C': 2}  
        },
        'A'
    )  
)
# answer : {'A': 0, 'B': 4, 'C': 3, 'D': 11, 'E': 1}

Dijkstra 한계

다익스트라는 두 정점을 잇는 간선들이 주어졌을 때, 그 중 가중치가 음수인 간선이 있으면 적용할 수 없습니다. 그 이유는 최소 비용의 음의 무한대 발산이 생길 수 있어 최소비용을 보장할 수 없기 때문입니다.

음수 가중치를 포함한 간선이 포함되었을 경우의 최소비용 문제는 Floyd Warshall 혹은 Bellman Ford 알고리즘을 사용할 수 있습니다.

다익스트라 유형

  1. 일반적인 다익스트라 (특정 시작점에서 모든 경로의 최단거리)
  2. 특정경로까지 갔다가 다시 되돌아오는 최단거리 (https://www.acmicpc.net/problem/1238)
  3. 특정한 경로들을 꼭 지나야하는 최단거리 (https://www.acmicpc.net/problem/1504)
  4. A ⇒ B 로 가는 가중치에 대한 간선의 정보가 여러가지 주어질때 (당연히 작은 가중치를 넣어야 함.)

Reference

Java 다익스트라 알고리즘(Dijkstra Algorithm)

백준 1504번(특정한 최단 경로) 문제 풀이

Recent Posts