행렬의 덧셈과 뺄셈
두개의 행렬이 주어졌을 때, 두 행렬의 합과 차는 두 행렬의 row 수와 col 수가 같아야 구할 수 있다.
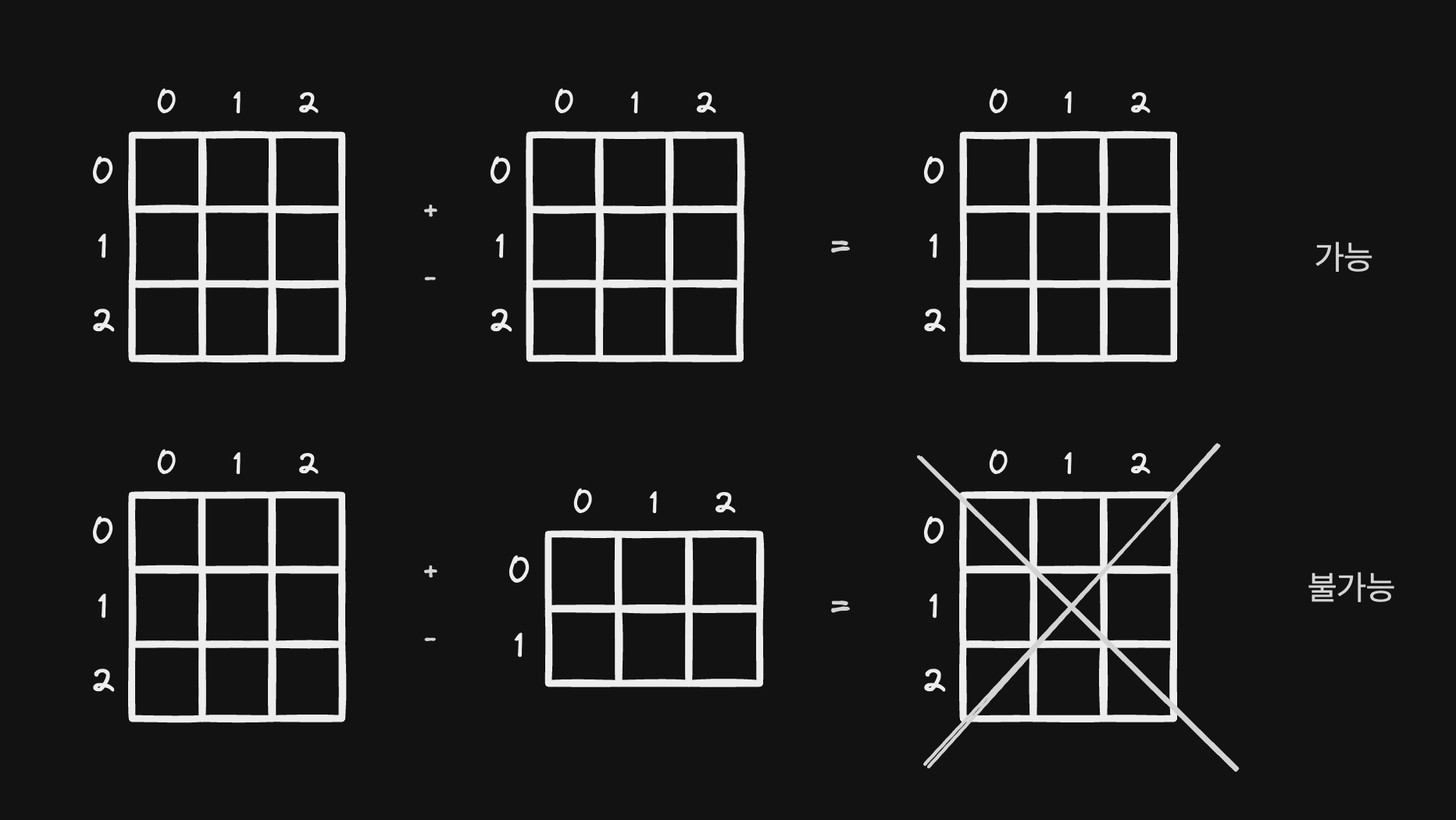
행렬의 합
두 행렬의 합은 매우 간단하다. 두 개의 행과 열의 수가 같아야하기 때문에 그냥 2 중 for 문으로 두 Matrix 의 값을 더해주면 된다.

def solution(arr1, arr2):
r_length, c_length = len(arr1), len(arr1[1])
answer = [[0] * c_length for _ in range(r_length)]
for row in range(r_length):
for col in range(c_length):
answer[row][col] = arr1[row][col] + arr2[row][col]
for row in range(r_length):
print(*answer[row])
solution(
[
[1,2,3],
[4,5,6],
[7,8,9],
],
[
[10,11,12],
[13,14,15],
[16,17,18]
]
)행렬의 차
두 행렬의 차도 앞서 적은 행렬의 덧셈과 부등호만 다른거 뺴고 같다.

def solution(arr1, arr2):
r_length, c_length = len(arr1), len(arr1[1])
answer = [[0] * c_length for _ in range(r_length)]
for row in range(r_length):
for col in range(c_length):
answer[row][col] = arr1[row][col] - arr2[row][col]
for row in range(r_length):
print(*answer[row])
solution(
[
[1,2,3],
[4,5,6],
[7,8,9],
],
[
[10,11,12],
[13,14,15],
[16,17,18]
]
)행렬의 곱셈
행렬의 곱셈은 덧셈과 뺄셈과 다르게, 두 행렬의 row 와 col 수가 달라도 구할 수 있다. 하지만 이에도 조건이 있는데 matrix1 이 2 행 3 열로 이루어진 (2 x 3) 구조라면, matrix2 는 3행 2열을 갖는 (3 x 2) 구조여야 한다. 좀더 정확히는 martrix1 의 열의 수와 matrix2 의 행의 수가 같아야 한다. 또한, 이 두 행렬의 곱 (2 x 3) * (3 x 2) 에 대한 결과 행렬은 matrix1 의 행과 matrix2 의 열인 (2 x 2) 구조가 나오게 된다.
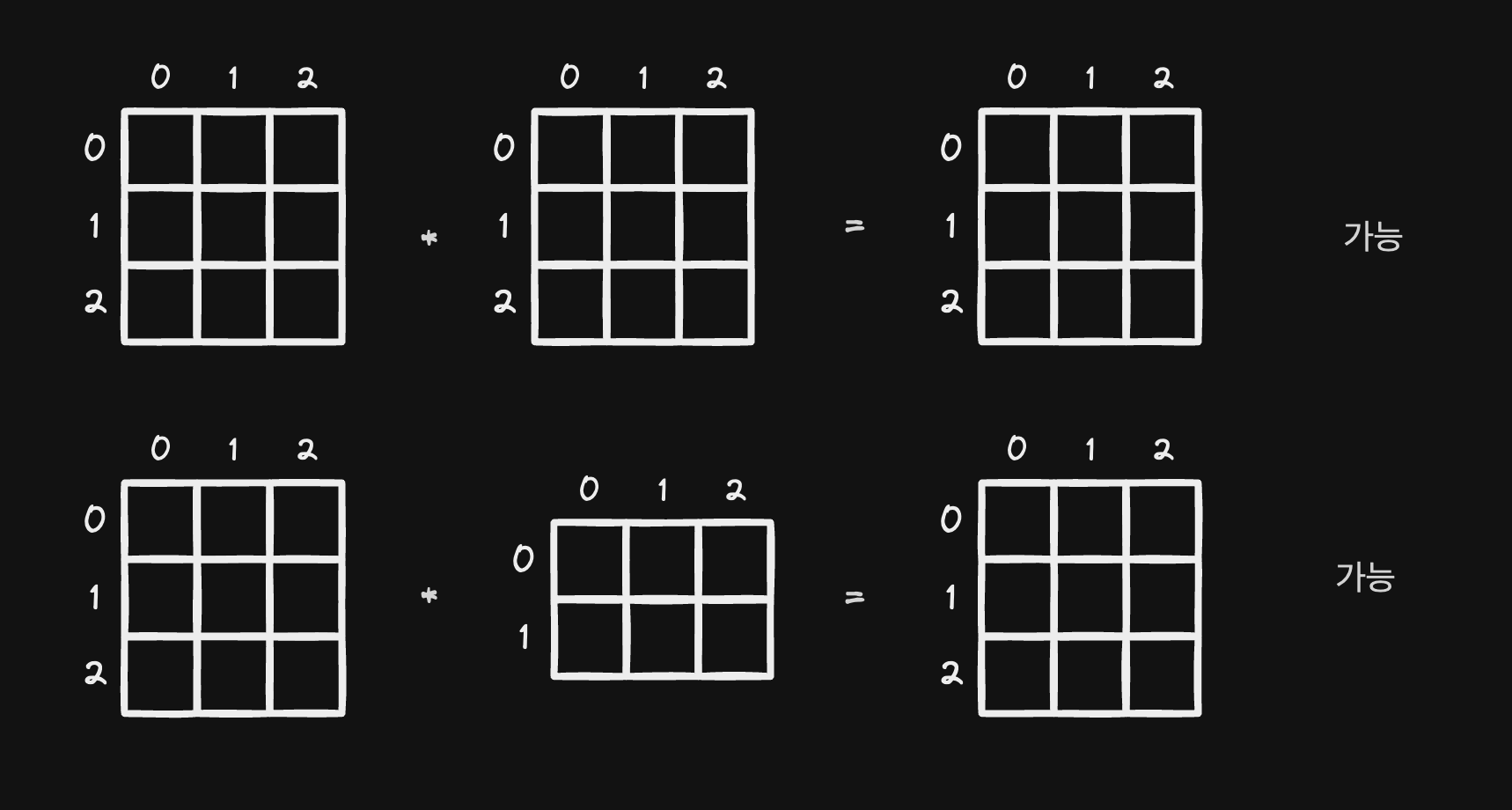
이게 matrix1 의 행과 matrix2 의 열을 곱해주면 된다.
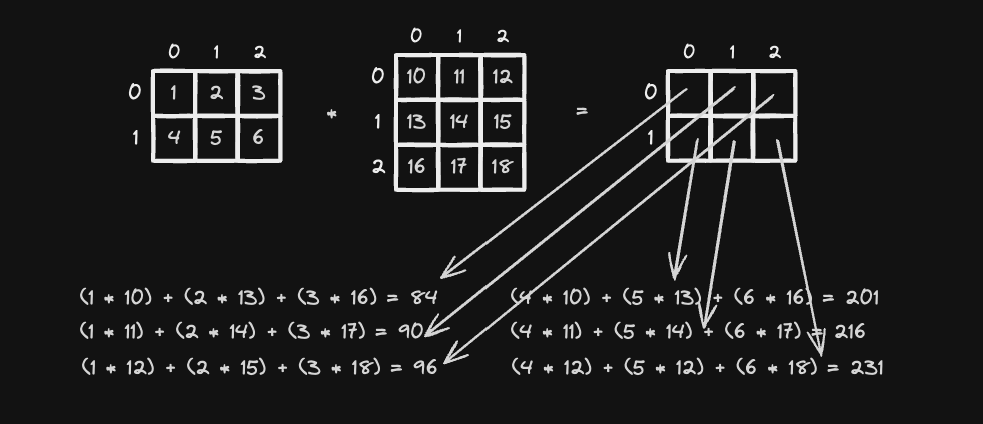
def solution(arr1, arr2):
arr1_row, arr1_col = len(arr1), len(arr1[1])
arr2_col = len(arr2[1])
answer = [[0] * arr2_col for _ in range(arr1_row)]
for n in range(arr1_row):
for k in range(arr2_col):
for m in range(arr1_col):
answer[n][k] += arr1[n][m] * arr2[m][k]
for line in answer:
print(*line)
solution(
[
[1,2,3],
[4,5,6]
],
[
[10,11,12],
[13,14,15],
[16,17,18]
]
)