Union Find
Union-Find 알고리즘은 그래프 알고리즘 중 하나로, 주로 서로소 집합(Disjoint Set) 을 관리할 때 사용됩니다. 이 알고리즘은 두 노드가 같은 집합에 속해 있는지 판별하거나, 두 개의 집합을 하나로 합치는 작업을 빠르게 처리할 수 있습니다.
서로소 집합은 겹치는 원소가 없는 집합들로, Union Find는 이러한 집합들을 효율적으로 관리할 수 있어 상호 배타적 집합(Disjoint Set Union, DSU)이라고도 불립니다.
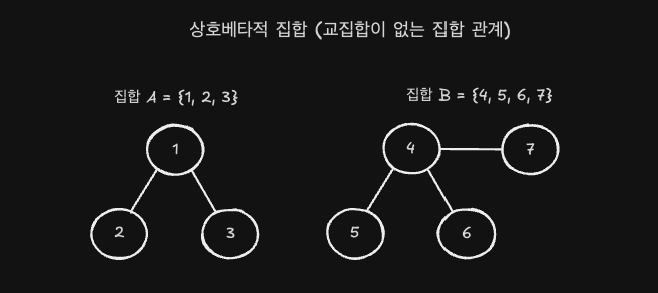
Union Find는 이름 그대로 두 가지 주요 연산으로 구성됩니다.
Union: 서로 다른 두 노드가 속한 집합을 하나의 집합으로 합치는(합집합) 연산을 말합니다.Find: 어떤 하나의 원소가 속하는 집합을 찾는 연산을 말합니다.
이 두 연산을 통해 다음과 같은 문제들을 해결할 수 있습니다.
- 두 노드가
같은 집합에 속하는지 여부확인 - 여러 노드들을 연결하면서
사이클 존재 여부판별 - 집합 간의
합병 및 그룹 분류
집합의 표현
Union-Find 알고리즘을 구현하기 위해서는 집합을 표현하는 방법을 알아야 합니다. 일반적으로 집합은 트리 구조로 표현하며, 이 트리는 배열을 통해 관리할 수 있습니다. 집합을 배열로 표현할 때, 각 집합에는 대표원소가 있어야 합니다. 트리의 각 노드는 부모 노드를 가리키고, 이 부모 관계를 따라 최상단에 있는 노드가 대표 원소(또는 루트 노드)가 됩니다.
이와 같은 구조를 통해, 집합의 병합(Union)이나 대표 노드 탐색(Find) 같은 연산을 효율적으로 수행할 수 있습니다.
대표원소
대표 원소는 하나의 집합을 대표하는 노드로, 해당 집합의 최상위 부모 노드(루트 노드) 를 의미합니다. 모든 노드가 이 대표 원소를 통해 동일한 집합에 속해 있음을 확인할 수 있습니다.
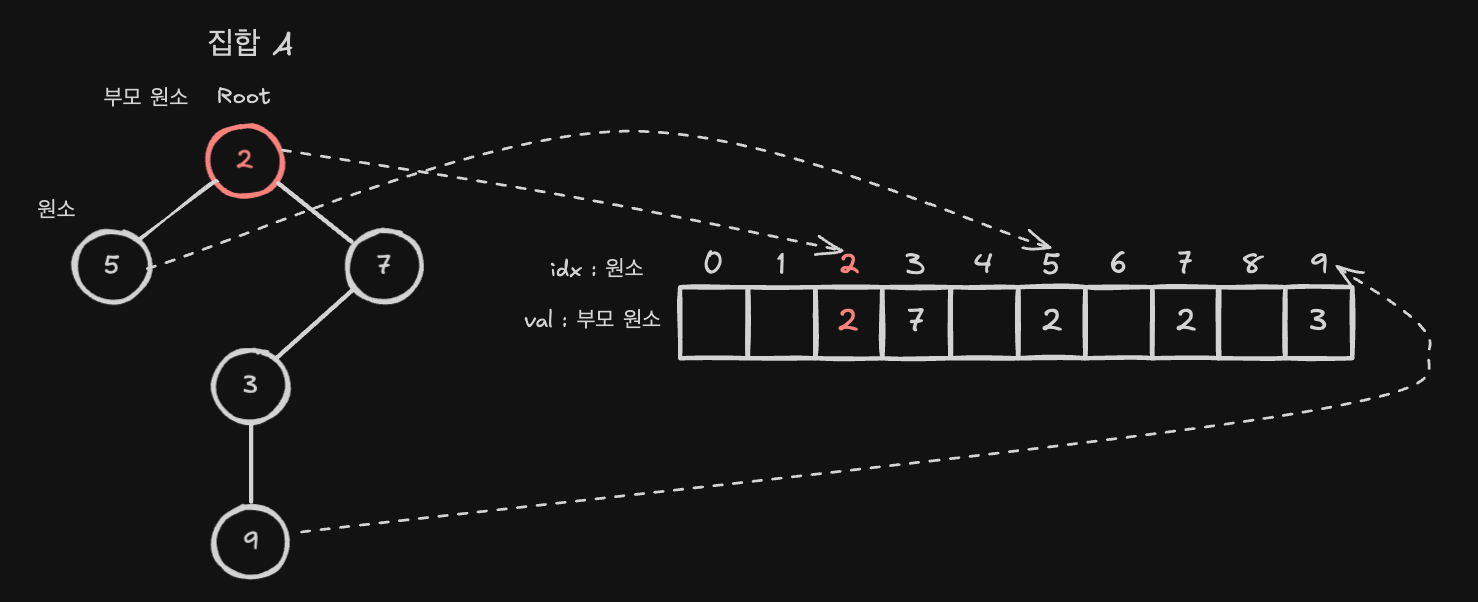
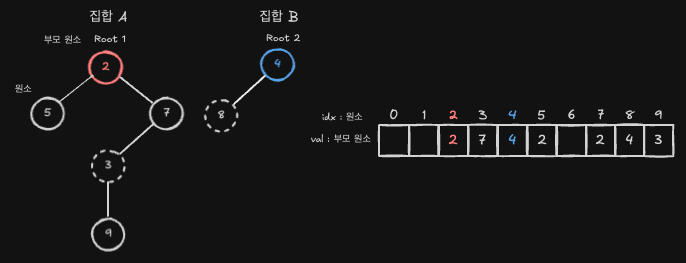
서로 다른 두 개의 집합을 트리 구조로 배열에 표현하는 예를 살펴보겠습니다. 먼저, 집합 A를 트리를 기반으로 배열로 나타내면 다음과 같습니다.
노드 2는 집합 A의 대표 원소이자 루트 노드입니다. 이 경우,Tree[2] = 2로 자기 자신을 가리킵니다.- 배열의
인덱스(Index)는 각 노드를 의미하고, 배열의값(Value)은 해당 노드의 부모 노드를 의미합니다. 즉, 의사코드로 표현하면Tree[현재 노드] = 부모 노드와 같습니다.
헷갈리지 않기 위해 사용되지 않는 노드는 배열에 값을 표현하지 않았습니다.
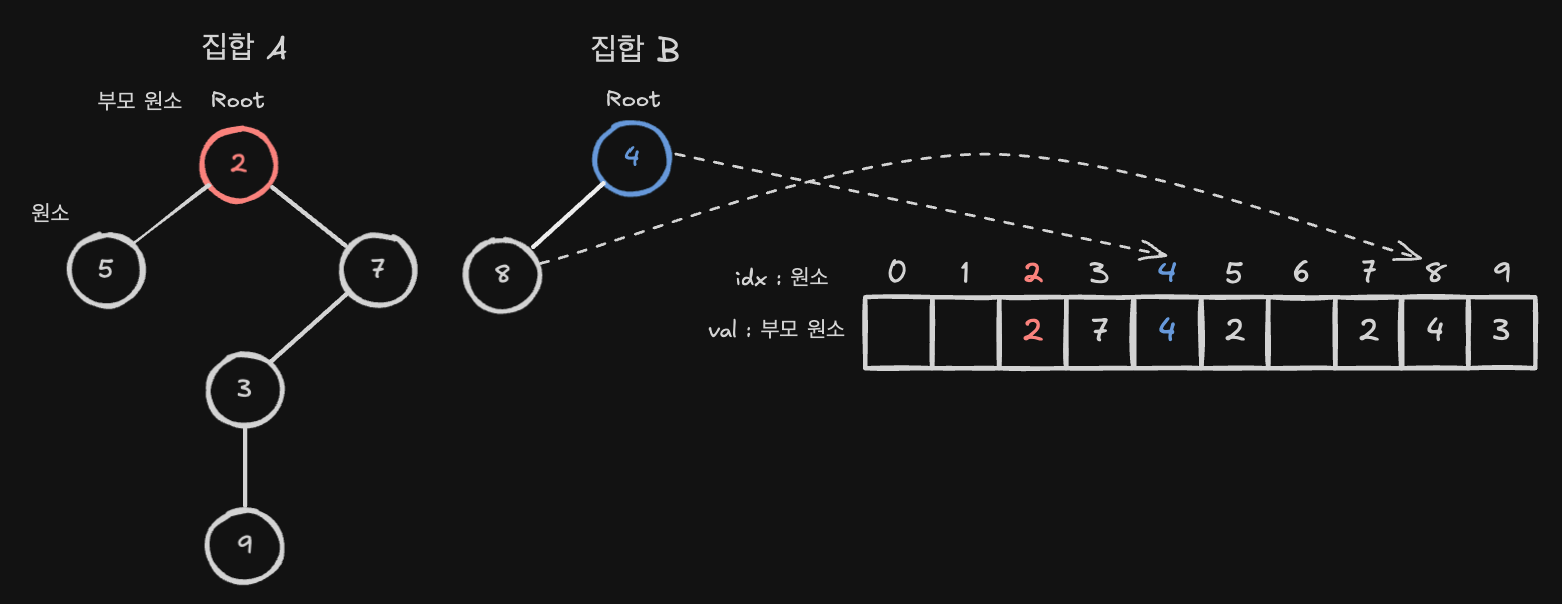
이 상태에서 집합 B 를 추가적으로 배열에 표현한다면 다음과 같이 나타낼 수 있습니다.
배열의 초기화
앞서 살펴본 것처럼, 서로 다른 두 집합을 하나의 배열에 표현할 수 있습니다. 그렇다면 이 배열은 처음에 어떻게 초기화해야 할까요?
- 배열의 크기는 집합을 구성하는 모든 원소들 중 가장 큰 값을 포함할 수 있도록 설정합니다.
- 배열의 초기값은
각 노드가 스스로를 부모로 가지도록 설정합니다. 이는 의사코드로 표현하면Tree[현재 노드] = 현재 노드와 같으며, 각 노드는 자신이 속한 집합의 대표 노드(루트 노드)가 자기 자신인 상태입니다. - 일반적으로
Index 0은 사용하지 않기 때문에 생략하거나-1같은 별도의 값으로 설정하기도 합니다. (사실 이 과정은 필수는 아니며, 그냥 두어도 무방합니다.)

Find 연산 과정
Find 연산은 특정 노드가 속한 집합의 대표원소(루트노드)를 찾는 연산입니다. Union 연산보다 Find 연산을 먼저 알아보는 이유는 Union 연산에서 Find 연산이 필요하기 때문입니다.
- 현재 노드에서 시작하여, 그 노드의 부모를 따라 계속 위로 올라갑니다.
- 이렇게 부모를 따라가다 보면,
자기 자신을 부모로 가지는 노드를 만나게 되는데, 이 노드가 바로 집합의대표원소(루트 노드)입니다.
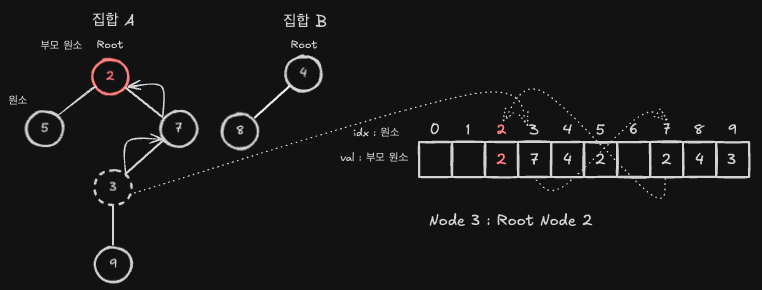
예를 들어, 노드 3이 속한 집합의 대표원소를 찾는 경우, 부모를 따라가면 3 → 7 → 2 순서로 올라가게 되며, 결국 2가 대표원소로 나옵니다.
Union 연산 과정
유니온 연산은 두 노드가 속한 서로 다른 두 집합을 하나의 집합으로 합치는 연산입니다.
- 먼저, 두 노드의 대표원소(Root 노드)를
Find연산을 통해 각각 찾습니다.- 이 때, 두 대표원소의 값이 같다면, 두 노드는 이미 같은 집합에 속해있다는 것을 의미합니다. 따라서 이 경우에는 Union 연산을 따로 수행하지 않아도 됩니다.
- 반대로 두 대표원소의 값이 다르면, 두 노드는 서로 다른 집합에 속해 있는 것이므로, 이 둘을 합칠 수 있습니다.
- 집합을 합칠 때는,
한쪽 대표 노드를 다른 쪽의 부모로 설정하여 트리를 연결합니다.- 물론 두 대표 원소가 같아도 Union 연산을 수행해도 무방하지만, 이는
불필요한 연산입니다. - 특히 사이클 여부를 판단하는 문제에서는 대표 원소가 다를 때만 Union 을 수행해야 사이클 생성을 정확히 탐지할 수 있습니다.
- 물론 두 대표 원소가 같아도 Union 연산을 수행해도 무방하지만, 이는
루트 노드 설정 기준
집합을 합칠 때는 한쪽 대표 노드를 다른 쪽의 부모로 설정하여 트리를 구성합니다. 이때 어느 쪽을 부모로 삼을지를 정하는 기준은 크게 두가지가 있습니다.
고정된 방향으로 합치기- 항상 root1 을 root2 의 부모로 정하거나 그 반대로 고정합니다.
- 이 방식은 두 집합을
합치는 순서에 따라 트리의 구조가 달라질 수 있습니다.
값의 크기를 기준으로 합치기- 대표 노드 중 값이 더 작은 쪽을 부모로 설정하거나, 그 반대로 합칩니다.
- 이 방식은 두 집합을 합치는 순서에 관계없이 트리의 구조가 일정합니다.
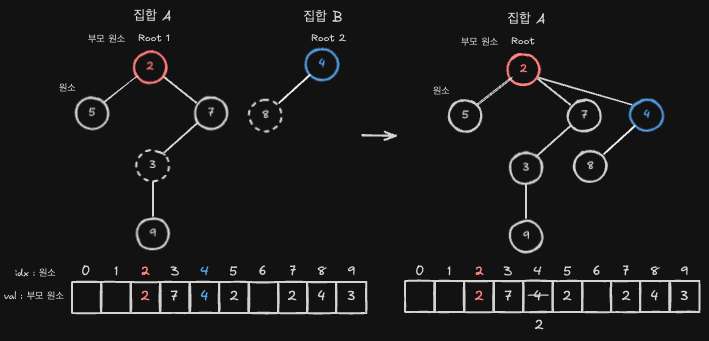
예를 들어, 아래 그림에서 노드 3과 노드 8이 속한 두 집합의 대표원소는 각각 2와 4입니다. 대표원소가 다르므로, 두 노드는 서로 다른 집합에 속해 있는 것을 알 수 있으며, 이제 두 집합을 하나로 합칠 수 있습니다.
여기서는 항상 root1을 root2의 부모로 설정하는 고정 방향 방식으로 집합을 합칩니다.
집합 A는 노드의 크기를 기준으로 정렬되지 않았기 때문에, 값의 크기를 기준으로 한 합치기 방식은 적절하지 않습니다. 따라서 합치는 순서에 따라 구조가 달라질 수 있지만, 예제의 일관성을 위해 고정 방식으로 처리합니다.
두 집합을 합치면 아래 결과가 나오게 됩니다. root1 이 root2 의 부모가 되어, root2 가 root1 하위로 들어간 것을 확인할 수 있습니다.
Implemention
파이썬으로 Union Find 는 다음과 같이 구현할 수 있습니다. 설명은 Comment 로 남겨두겠습니다.
def solution(mx_node, edges, s1, s2):
def find(n):
if tree[n] == n:
return n
return find(tree[n])
def union(n1, n2):
root1, root2 = find(n1), find(n2)
if root1 != root2: # 사이클을 생성 여부를 판단하는 것이 아니면 불필요함.
tree[root2] = root1
tree = list(range(mx_node + 1)) # Tree 배열로 초기화
for n1, n2 in edges: # Edges 들로 집합 A B 구성
union(n1, n2)
print('before :', *tree[1:], sep=' ') # n1 n2 합치기 전 Tree 배열 확인
union(s1, s2)
print('after :', *tree[1:], sep=' ') # n1 n2 합친 후 Tree 배열 확인
mx_node = 9 # 모든 집합을 이루는 노드들 중 가장 큰 값
edges = [
[3, 9],
[7, 3],
[2, 7],
[2, 5], # 여기까지 집합 A 구성 (집합을 구성하는데도 union 사용)
[4, 8] # 여기까지 집합 B 구성 (집합을 구성하는데도 union 사용)
]
s1 = 3 # 노드 3
s2 = 8 # 노드 8
solution(mx_node, edges, s1, s2)output 은 아래와 같이 나옵니다 앞서 살펴본 예제와 동일한 결과임을 확인할 수 있습니다.
before : 1 2 7 4 2 6 2 4 3
after : 1 2 7 2 2 6 2 4 3성능 문제
하지만 해당 코드의 find 함수에는 성능 이슈가 있습니다. 현재 코드는 트리의 깊이가 클 경우, 특히 Degenerate Tree처럼 한쪽으로 치우친 구조에서는 O(N)까지 시간이 걸릴 수 있습니다. 이 문제를 해결하기 위해 다음 두 가지 기법을 적용할 수 있습니다.
- Path Compression (경로 압축)
- find 연산 시, 방문한 모든 노드가
직접 루트를 가리키도록 설정해서 다음 find를 더 빠르게 수행하게 만듭니다.
- find 연산 시, 방문한 모든 노드가
- Union By Rank (랭크 기반 유니온)
- 항상
더 작은 트리를 더 큰 트리 밑에 붙여서 트리의 깊이를 최소화합니다. - 보통
rank는 트리의 “깊이”나 “크기”를 의미하는 배열을 따로 만들어 관리합니다.
- 항상
이에 대한 내용은 다음 시간에 알아보도록 하겠습니다.