Graph
Graph(그래프) 는 노드와 간선으로 이루어진 비선형 데이터 구조입니다.
- 그래프는 데이터간의 연결관계를 표현하는데 사용됩니다.
데이터는 노드(Node)로,노드간의 관계나 흐름을 간선(Edge)으로 표현합니다. 만약 관계나 흐름의 정도를 표현할 필요가 있다면 간선에 Weight(가중치) 라는 개념을 추가하여 표현합니다. - 그래프는 방향이 있는
Directed Graph의 형태로 구성될 수 있고, 방향이 없는Undirected Graph형태로 구성될 수 있습니다. - 그래프는 순환이 있는 형태의
Cyclic Graph형태로 구성될 수 있고, 순환이 없는Acyclic Graph형태로 구성될 수 있습니다. - 그래프는
연결 그래프(Connected Graph)일 수 있으며, 여러개의고립된 부분 그래프(Isolated Subgraphs)로 나뉜비연결 그래프 (Disconnected Graph)일 수 있습니다. - 그래프를 탐색 및 순회하는 방법에는 대표적으로 BFS(Breadth First Search) 와 DFS(Depth First Search) 가 있습니다.
Graph 의 유형
방향 그래프 & 무방향 그래프
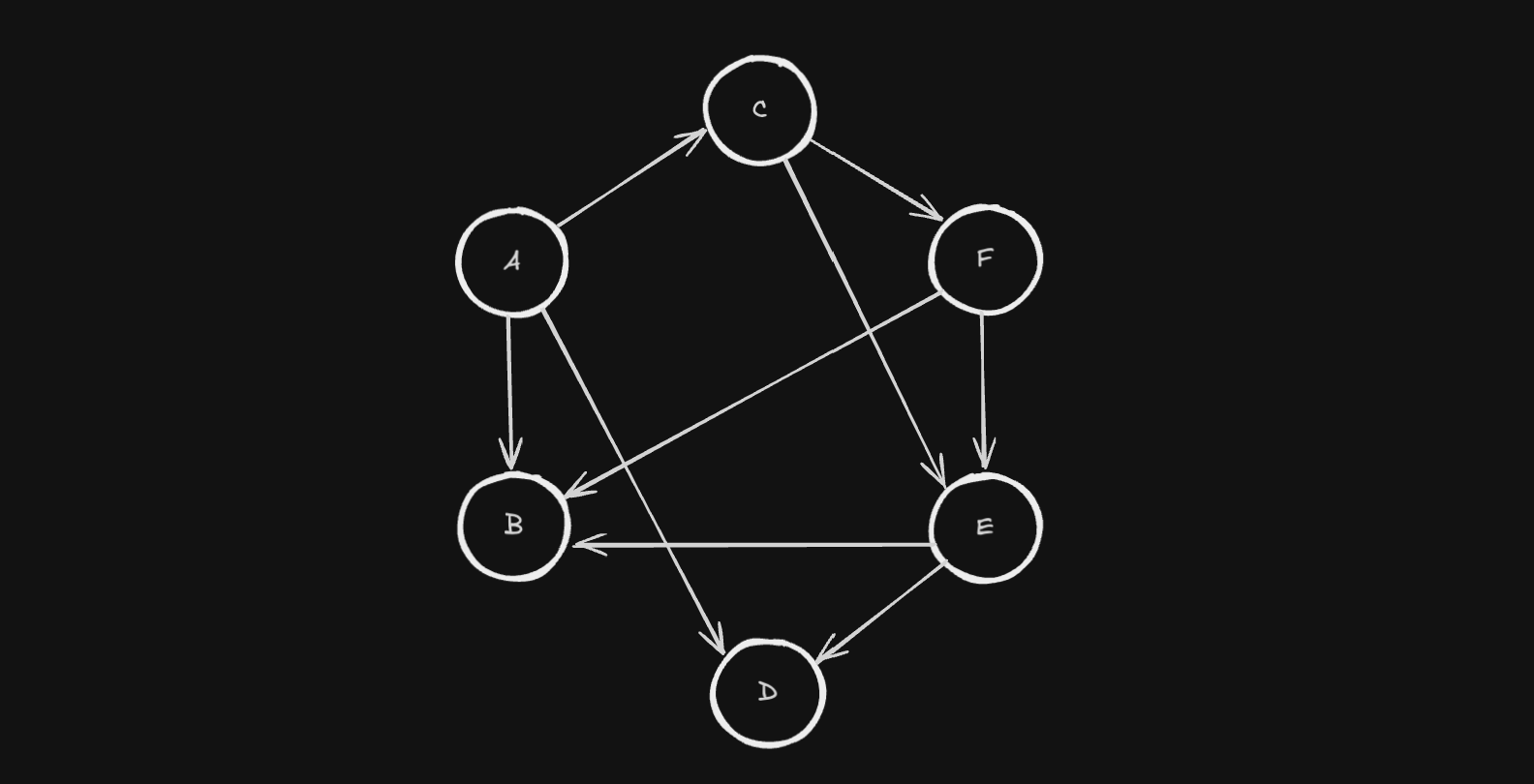
Directed Graph(방향 그래프 : 유향 그래프)는 노드간의 관계를 표현하는 간선에 방향성이 있는 그래프를 말합니다. 간선으로 연결된 두개의 노드간의 이동은 단방향으로만 이루어집니다.
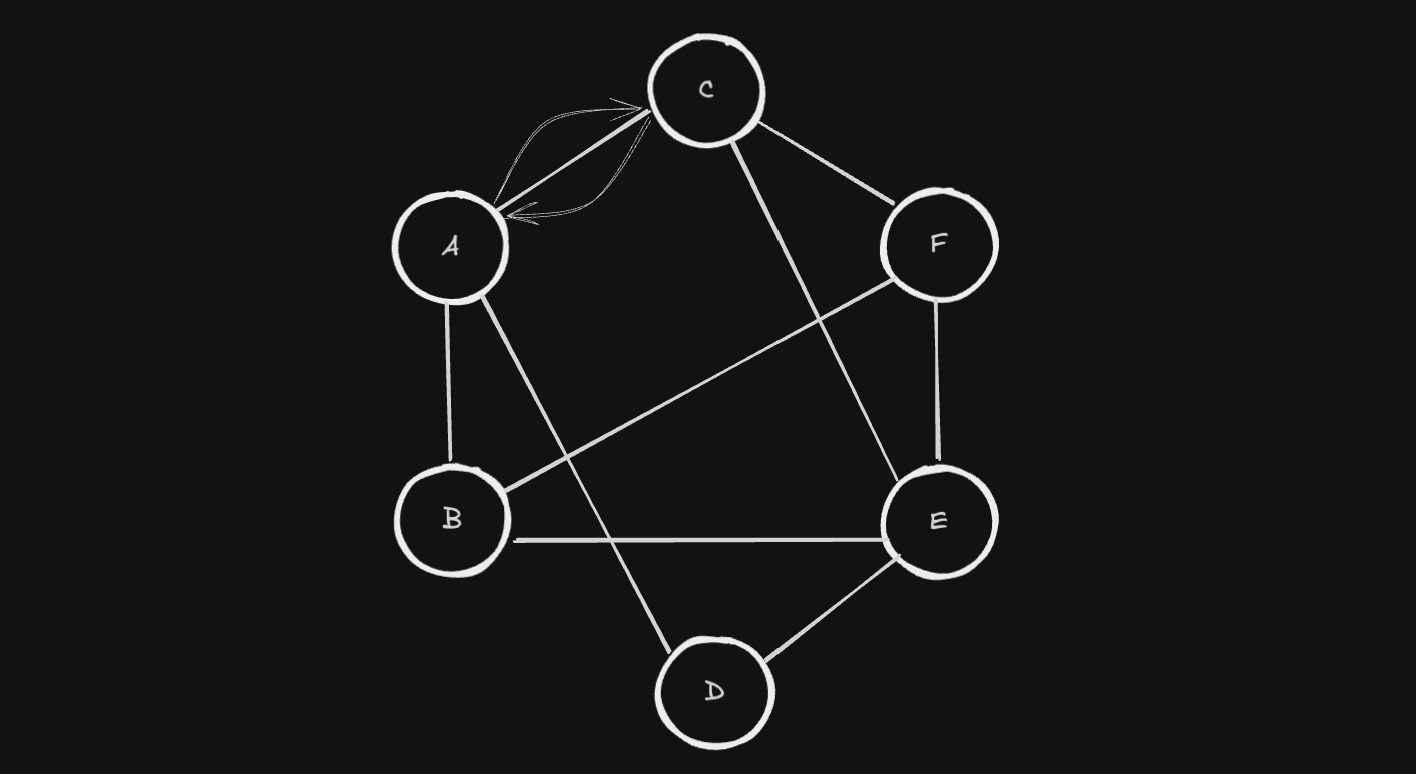
Undirected Graph(무방향 그래프 : 무향 그래프)는 노드간의 관계를 표현하는 간선에 방향성이 없는 그래프를 말합니다. 간선으로 연결된 두개의 노드간의 이동은 양방향으로 이루어집니다.
가중치 그래프
Weight Graph(가중치 그래프)는 두 정점을 연결하는 간선에 가중치(Weight)가 할당된 그래프를 말합니다.
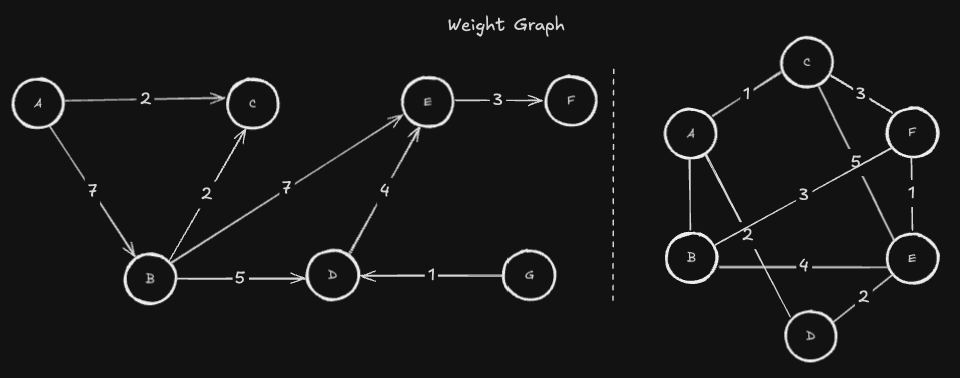
순환 그래프 & 비순환 그래프
Cycle Graph(순환 그래프)는 어떤 정점 v 에서 시작하여 간선을 따라 이동한 뒤 다시 v로 돌아오는 단순 순환 경로만으로 구성된 그래프를 말합니다.
순환
순환이란 하나의 정점에서 출발하여 간선을 따라 이동하다가 처음 정점으로 되돌아오는 경로를 의미하며, 이때 경로 중 동일한 정점이나 간선은 처음과 끝을 제외하고 한 번만 등장해야 합니다. 즉, 순환 여부는 노드의 중복 방문 여부로 판단합니다.
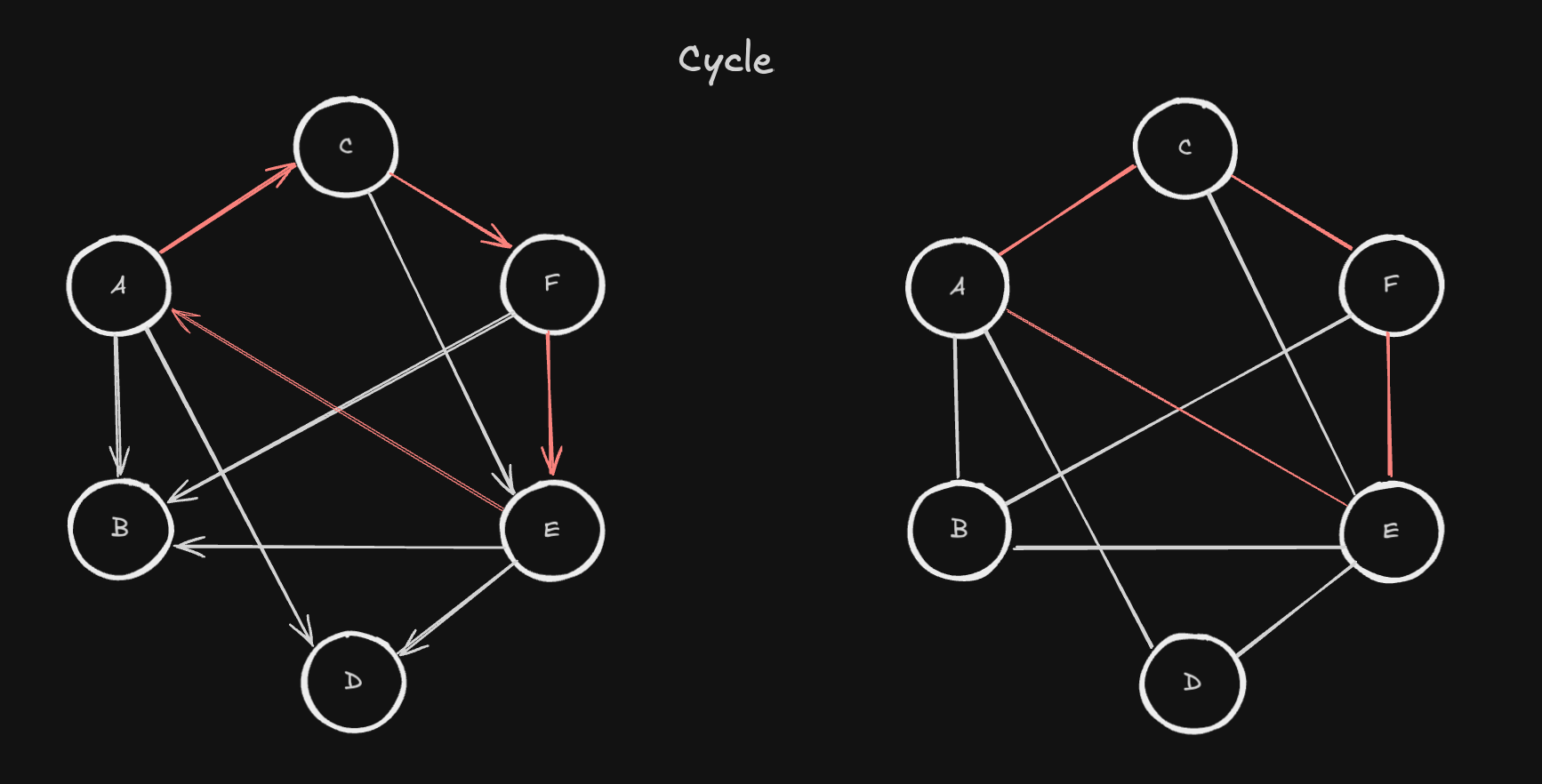
Acyclic Graph(비순환 그래프)는 어떤 정점 v 에서 시작해 간선을 따라 이동하더라도, 다시 v 로 돌아오는 순환 경로가 존재하지 않는 그래프를 말합니다.
- 왼쪽 그래프는 방향 그래프의 어떤 정점에서 출발해서 다시 자기 자신으로 돌아오는 경로(Cycle)가 전혀 없기 때문에
방향 비순환 그래프(Directed Acyclic Graph : DAG)라고 합니다. - 오른쪽 그래프는 트리입니다. 트리는 방향이 존재하지 않고, 순환이 발생하지 않는 비순환 그래프의 종류 중 하나입니다.

연결 그래프 & 비연결 그래프
연결 그래프(Connected Graph)는 모든 노드가 하나의 연결된 컴포넌트로 이루어져 어떤 두 노드간에 간선이 존재하는 그래프를 말합니다.
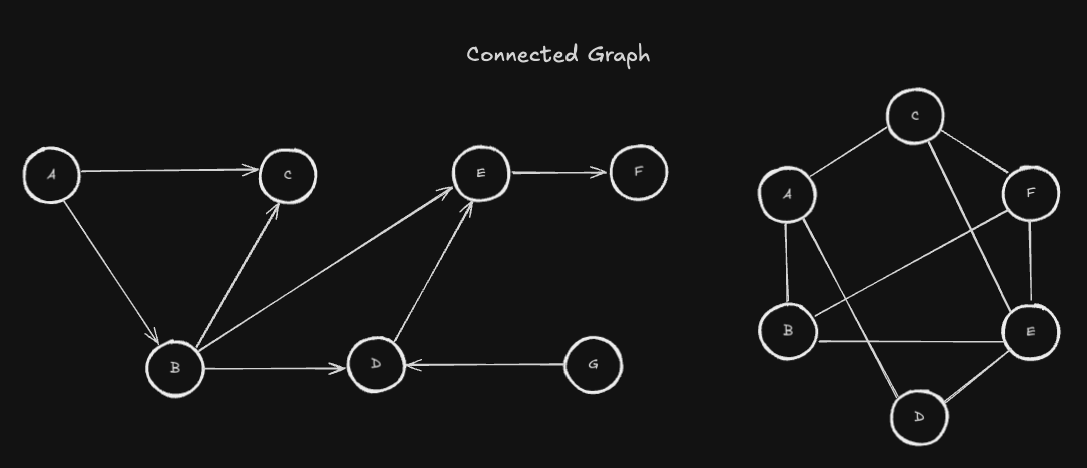
비연결 그래프(Disconnected Graph)는 모든 노드가 하나의 연결된 컴포넌트를 이루지 않고, 여러개의 고립된 부분 그래프(Isolated Subgraphs) 로 구성된 그래프를 말합니다.
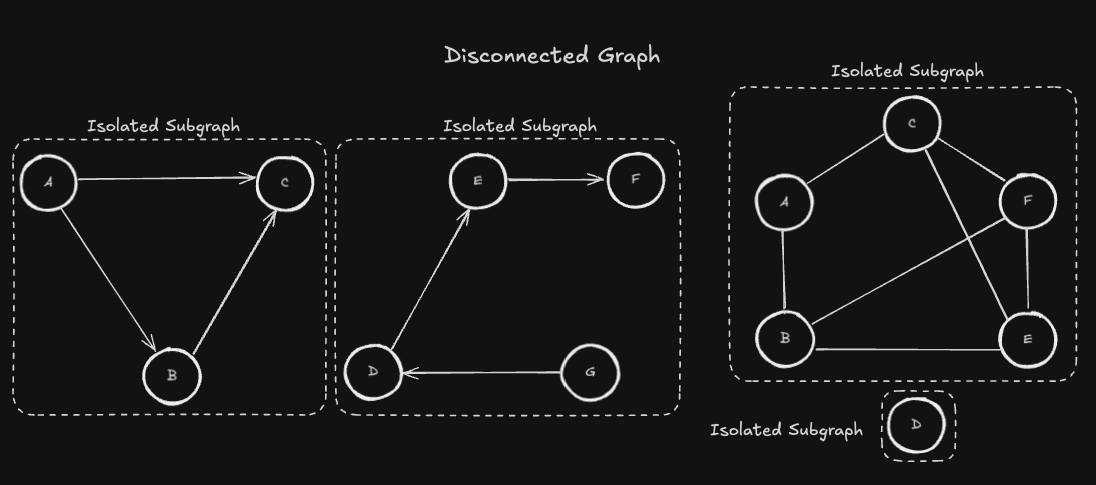
완전 그래프
Complete Graph(완전 그래프)는 각 정점에서 자기 자신을 제외한 다른 모든 정점을 연결하여 가능한 최대의 간선 수를 가진 그래프를 말합니다. 만약 그래프를 구성하는 노드의 수가 N 이라면
- 무방향 그래프에서의 최대 간선의 수는
N(N - 1) / 2입니다. - 방향 그래프에서의 최대 간선의 수는 두 정점에 대하여 다른 두개의 간선을 연결할 수 있으므로
N(N - 1)입니다.

이분그래프
Bipartite Graph(이분그래프)는 인접한 정점끼리 서로 다른 그룹으로 분류하여 모든 정점을 두 가지 그룹으로만 분류할 수 있는 그래프를 말합니다. 인접한 정점끼리 서로 다른 그룹으로 분류하기 때문에 같은 그룹의 정점끼리는 간선으로 이어지지 않습니다.
Note
간선이 아예 없고 정점만 있는 경우도 이분 그래프입니다.
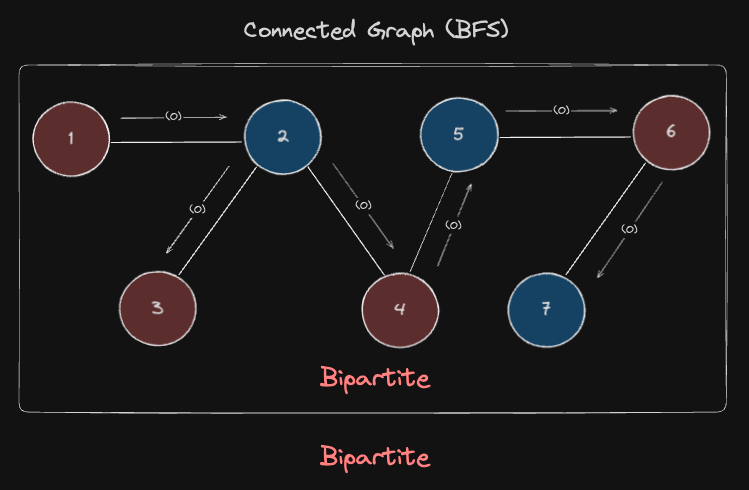
하지만 그래프가 비연결 그래프(Disconnected Graph)로 주어질 수 있기 때문에, 이분 그래프인지 판단할 때 여러개로 나뉘어진 고립된 부분 그래프(Isolated Subgraphs)들도 모두 이분 그래프인지 확인해야합니다. 그래프를 이루는 여러개의 부분그래프 중 단 하나라도 이분그래프가 아님이 증명되면, 그 그래프는 이분 그래프가 아니게 됩니다.
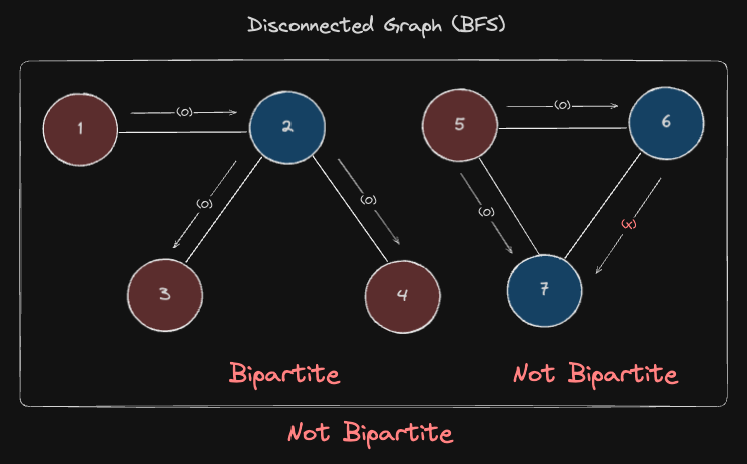
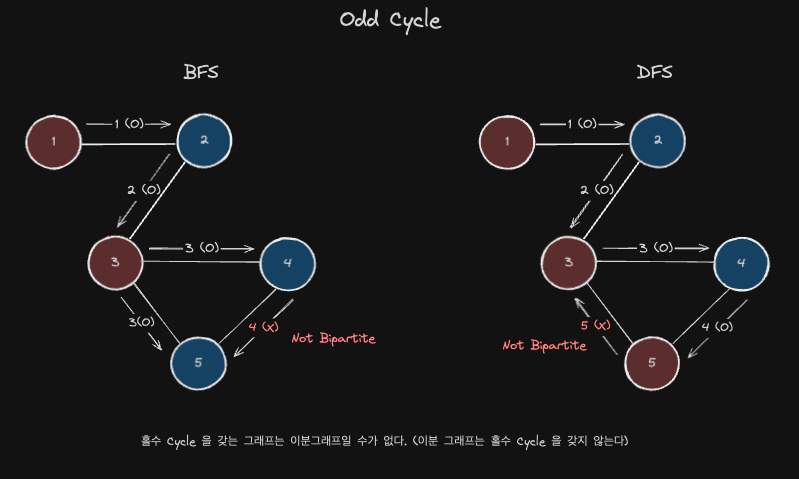
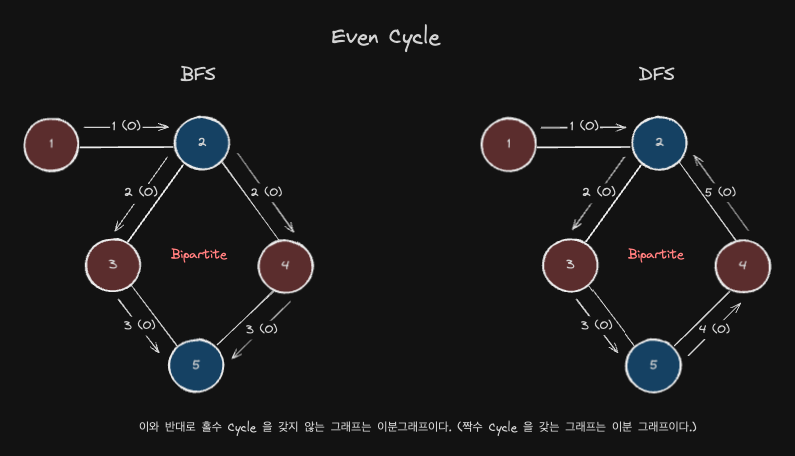
또한 주어진 그래프가 Cycle을 형성할 수 있습니다. 이러한 경우에는 Cycle 을 이루는 노드의 개수를 세어 Odd Cycle(홀수 사이클) 인지 Even Cycle (짝수 사이클) 인지 확인하면 됩니다. Odd Cycle 이면 이분그래프일 수 없고, Even Cycle 이면 이분그래프입니다.