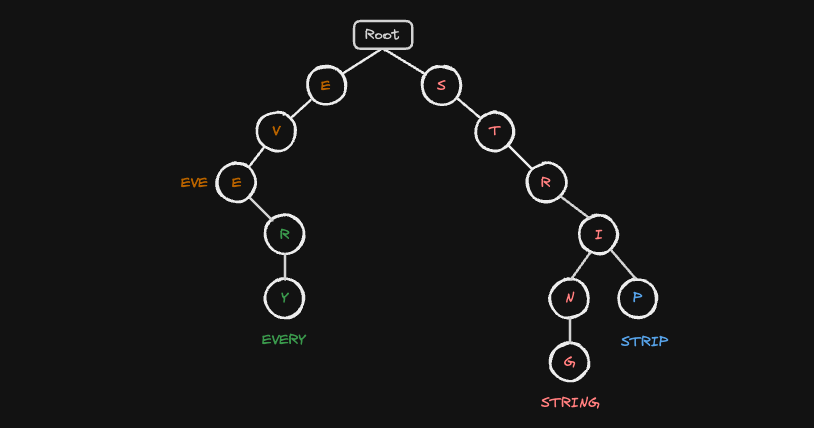
Trie

트라이(Trie)는 문자열을 저장하고 효율적으로 탐색하기 위한 m-ary 트리 형태의 자료구조입니다.

트라이를 구성하는 각 노드는 하나의 문자(Character)를 표현하며, 문자열 전체는 루트에서 리프까지의 경로로 표현되기 때문에, 특정 문자열 또는 접두사를 찾는 연산이 매우 직관적이고 빠릅니다.
각 노드의 자식 노드는 보통 고정 크기 배열(알파벳 수) 또는 해시맵(동적)으로 표현됩니다.

루트에서 특정 노드까지의 경로가 문자열의 접두사(Prefix)를 그대로 나타내므로 Prefix Tree라고도 불립니다.

Operation

트라이에는 크게 4가지 연산이 있습니다. 각 연산과 시간복잡도는 아래와 같습니다.

아래 표는 각 노드의 자식들을 Dictionary(HashMap)으로 표현했을 때의 시간 복잡도를 말합니다.

Operation	Time	Description
삽입(Insert)	O(S)	S는 문자열의 길이를 말합니다. 각 문자를 한 번씩 따라가며 노드를 생성 및 이동합니다.
탐색(Search)	O(S)	문자열의 각 문자를 따라가며 존재 여부 확인합니다.
삭제(Erase)	O(S)	존재 여부 확인 후, 필요 시 하위 노드 제거합니다. (후위 순회 또는 스택 기반)
접두사 확인 (StartsWith)	O(P)	P는 접두사의 길이를 말합니다.

Insert

Insert는 트라이에 문자열을 삽입하는 연산입니다. 각 문자를 따라 노드를 만들며, 마지막 문자에서 종료 표시(terminal)를 남깁니다.

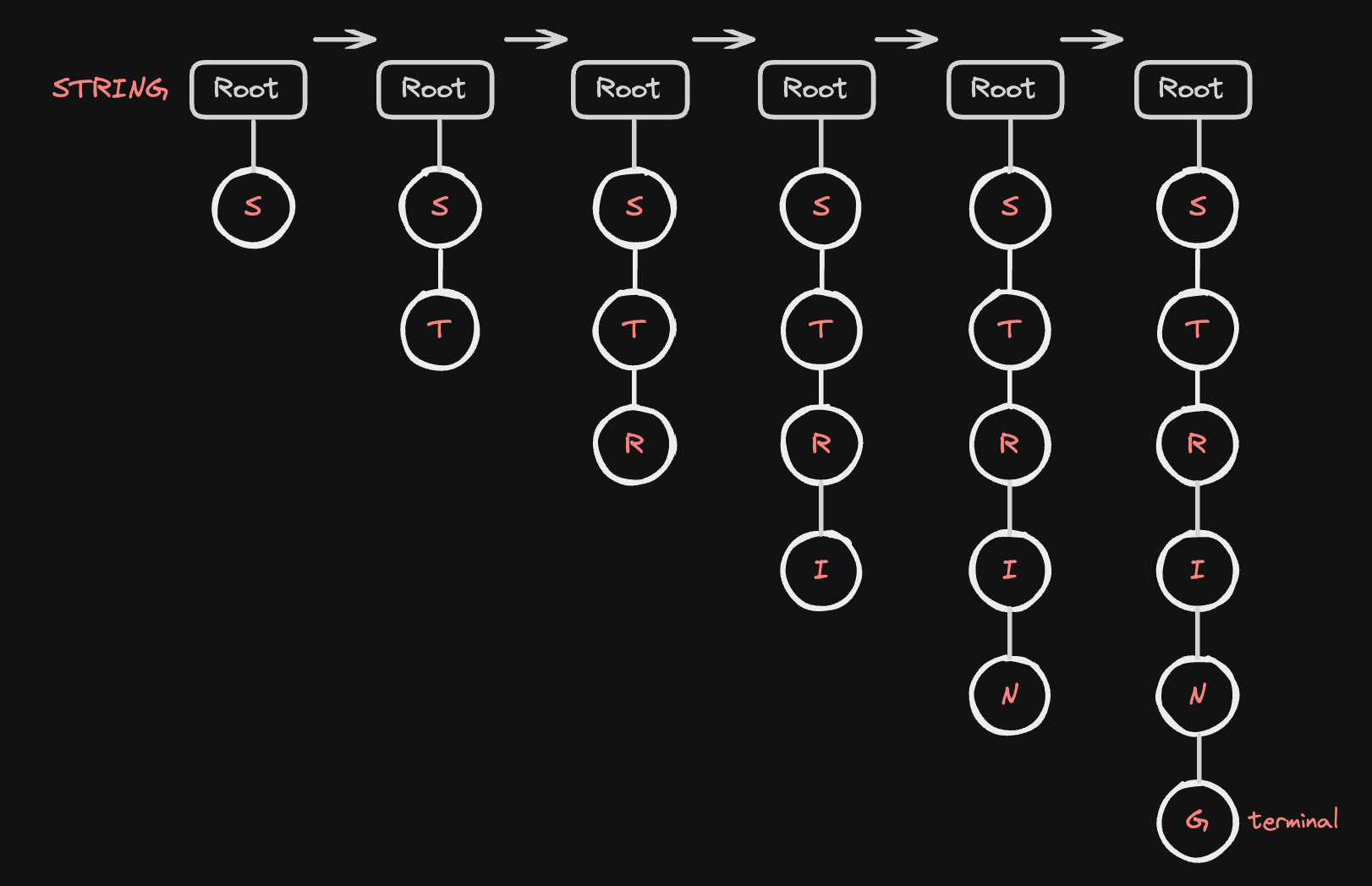
가장 먼저 STRING 문자열을 트라이에 삽입하는 과정을 보겠습니다.

S: 루트 노드의 자식에 자식 노드가 한개도 없습니다. 따라서 문자 S에 해당하는 노드를 생성하여 루트 노드의 자식으로 추가하고 해당 노드로 이동합니다.
T: S 노드의 자식 중에 T 노드는 없습니다. 따라서 T 노드를 생성하고 S의 자식으로 추가하고 해당 노드로 이동합니다.
R: T 노드의 자식 중에 R 노드는 없습니다. 따라서 R 노드를 생성하고 T의 자식으로 추가하고 해당 노드로 이동합니다.
I: R 노드의 자식 중에 I 노드는 없습니다. 따라서 I 노드를 생성하고 R의 자식으로 추가하고 해당 노드로 이동합니다.
N: I 노드의 자식 중에 N 노드는 없습니다. 따라서 N 노드를 생성하고 I의 자식으로 추가하고 해당 노드로 이동합니다.
G: N 노드의 자식 중에 G 노드는 없습니다. 따라서 G 노드를 생성하고 N의 자식으로 추가합니다.
- 마지막 문자이므로, 해당 노드에 terminal = True로 표시합니다.

STRIP 문자열을 트라이에 삽입하겠습니다.

S: 루트 노드의 자식 중에 S 노드가 이미 존재하므로 해당 노드로 이동합니다.
T: S 노드의 자식 중에 T 노드가 이미 존재하므로 해당 노드로 이동합니다.
R: T 노드의 자식 중에 R 노드가 이미 존재하므로 해당 노드로 이동합니다.
I: R 노드의 자식 중에 I 노드가 이미 존재하므로 해당 노드로 이동합니다.
P: I 노드의 자식 중에 P 노드가 존재하지 않으므로 새로 생성하여 추가합니다.
- 마지막 문자이므로 terminal = True로 표시합니다.

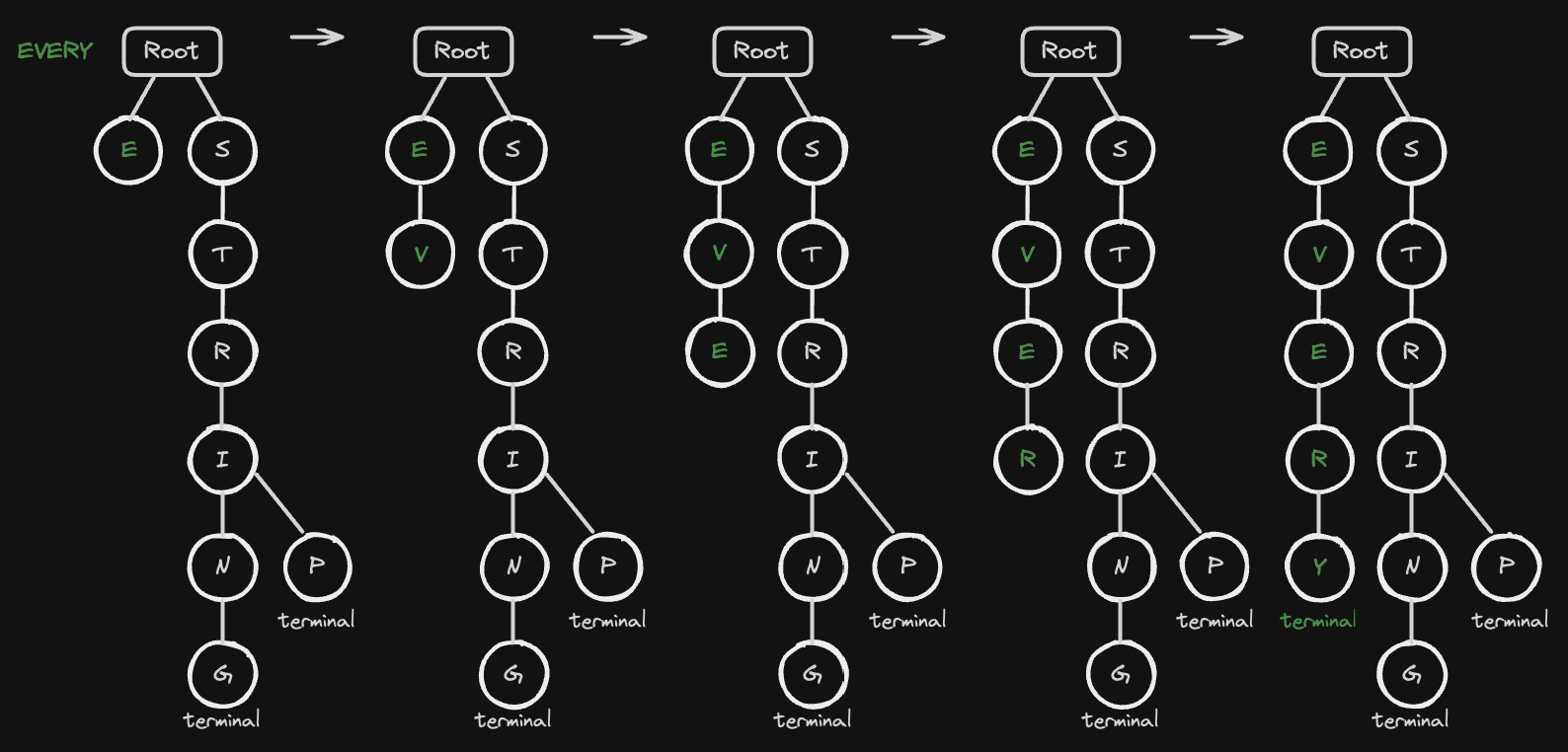
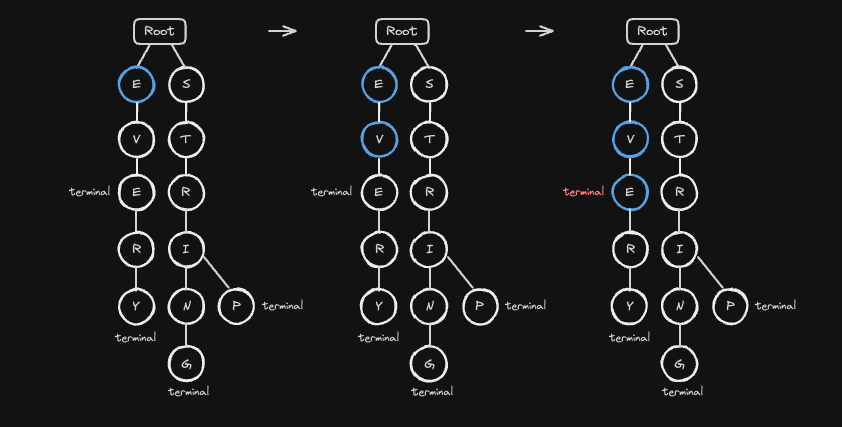
EVERY 문자열을 트라이에 삽입하겠습니다.

E : 루트 노드의 자식 중에 E 노드가 존재하지 않으므로 새로 생성하여 추가합니다.
V : E 노드의 자식 중에 V 노드가 존재하지 않으므로 새로 생성하여 추가합니다.
E : V 노드의 자식 중에 E 노드가 존재하지 않으므로 새로 생성하여 추가합니다.
R : E 노드의 자식 중에 R 노드가 존재하지 않으므로 새로 생성하여 추가합니다.
Y : R 노드의 자식 중에 Y 노드가 존재하지 않으므로 새로 생성하여 추가합니다.
- 마지막 문자이므로 해당 노드에 terminal = True로 표시합니다.

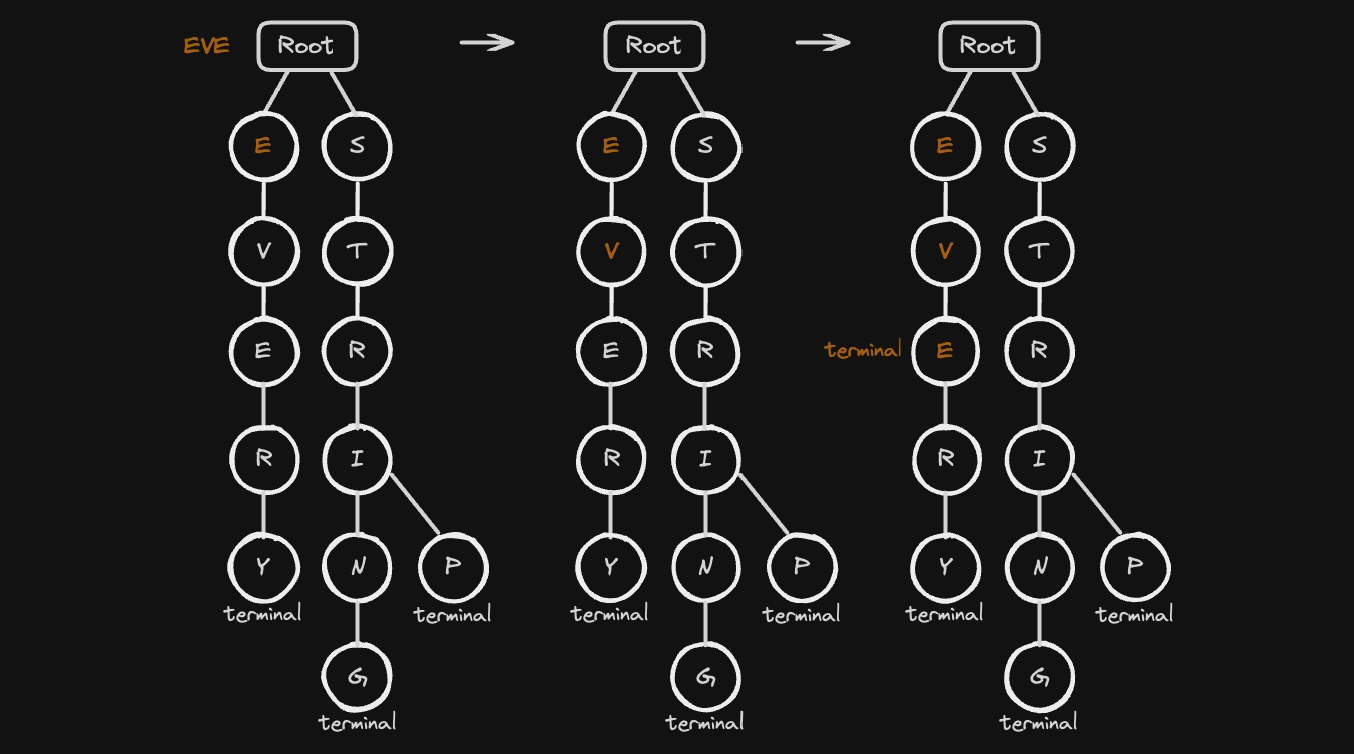
마지막 문자열 EVE 문자열을 트라이에 삽입하겠습니다.

E : 루트 노드의 자식 중에 E 노드가 이미 존재하므로 해당 노드로 이동합니다.
V : E 노드의 자식 중에 V 노드가 이미 존재하므로 해당 노드로 이동합니다.
E : V 노드의 자식 중에 E 노드는 존재하지 않으므로 새로 생성하여 추가합니다.
- 마지막 문자이므로 해당 노드에 terminal = True로 표시합니다.

Search

Search는 트라이에 해당 문자열이 존재하는지 확인하는 연산입니다. 각 문자를 따라 내려가며, 마지막 문자가 종료 노드인지 검사합니다.

EVE 문자열이 트라이에 존재하는지 확인해보겠습니다.

E : 루트 노드의 자식 중에 E 노드가 존재하므로 해당 노드로 이동합니다.
V : E 노드의 자식 중에 V 노드가 존재하므로 해당 노드로 이동합니다.
E : V 노드의 자식 중에 E 노드가 존재하므로 해당 노드로 이동합니다.
- 해당 노드는 terminal = True로 설정되어 있으므로, "EVE"는 트라이에 존재합니다.

Erase

Erase는 특정 문자열을 트라이에서 제거하는 연산입니다. 문자열을 제거하는 방법은 두 가지가 있습니다.

문자열의 각 문자를 따라 마지막 노드까지 내려간 후, 해당 노드의 종료 표시(terminal)만 제거합니다. 구조는 그대로 유지되지만, 더 이상 해당 문자열은 유효한 단어로 인식되지 않게 됩니다. 실제로 노드를 삭제하지 않기 때문에 메모리 효율은 다소 떨어질 수 있습니다.
마지막 노드의 종료 표시를 제거한 후, 해당 노드부터 역방향으로 올라가며 더 이상 다른 문자열과 공유되지 않는 노드를 제거합니다. 이때 다른 단어와 경로를 공유하는 노드는 그대로 유지되고, 단독으로만 사용된 경로만 삭제됩니다.

STRING 문자열을 제거하는 과정을 보겠습니다. 우선 각 문자를 따라 마지막 노드인 G노드까지 내려갑니다. G노드는 종료 표시(terminal=True)가 되어 있으므로, 이를 해제하여 해당 단어를 트라이에서 논리적으로 제거합니다.

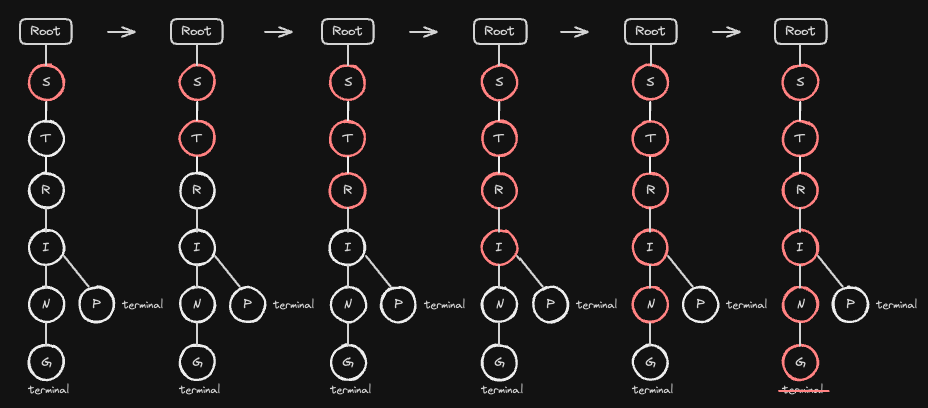
그 다음, G 노드부터 역방향으로 올라가며 삭제 조건을 확인합니다. 조건은 "해당 노드가 종료 노드가 아니며, 자식 노드가 없는 경우" 입니다.

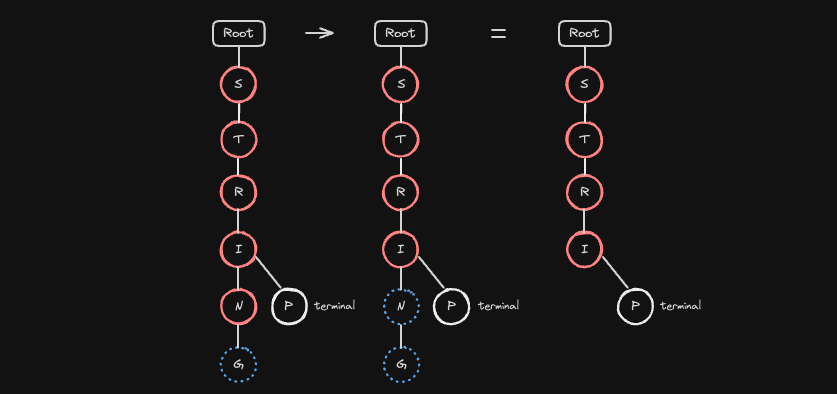
G 노드는 자식이 없고, 종료 표시도 해제되었으므로 삭제됩니다.
N 노드도 자식이 없고 종료 표시가 없으므로 삭제됩니다.
I 노드는 terminal 표시가 되어 있고, 동시에 다른 문자열(“STRIP”)과 경로를 공유하고 있기 때문에 삭제하지 않습니다.

StartsWith

StartsWith는 특정 문자열로 시작하는 단어가 트라이에 존재하는지 확인하는 연산입니다. Search와 매우 유사해 보이지만, 아래 차이점이 존재합니다.

Search는 마지막 노드가 종료 노드(terminal)인지 확인하지만,
StartsWith는 단순히 문자 경로가 존재하는지만 확인합니다.

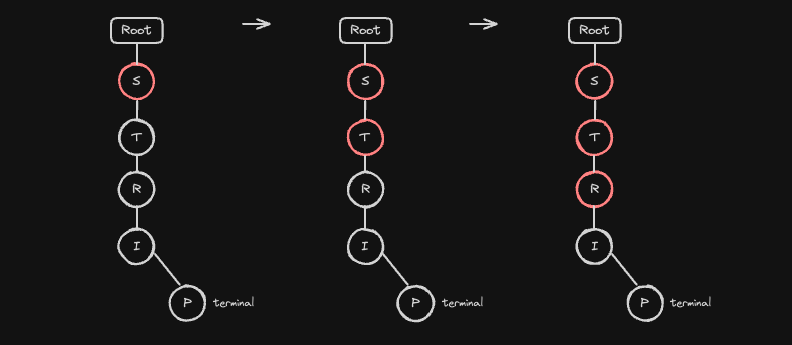
즉, 주어진 문자열이 트라이 상의 경로로 존재하는지만 검사하고, 실제 단어로 등록되어 있는지 여부는 확인하지 않습니다. 예를 들어 STR로 시작하는 단어가 트라이에 있는지 확인하는 과정을 보겠습니다.

우선 각 문자를 따라 마지막 노드인 R노드까지 내려갑니다.
R 노드에 종료 표시(terminal)가 없더라도, 경로 자체가 존재하기 때문에 True를 반환하게 됩니다.

반대로 Search(“STR”)를 수행하면 False가 반환됩니다. Search는 마지막 노드(R)에 Terminal 표시가 되어 있는지 여부를 확인하기 때문입니다.

Implementation

Trie를 구성하는 각 노드는 자신이 종료노드인지 확인할 수 있는 terminal 필드와 자식들을 나타내는 children 필드가 필요합니다. 또한, 자식들은 Dictionary로 표현할 수 있습니다. 각 연산에 대한 과정을 위에서 충분히 설명했기 때문에, 코드는 별도의 설명 없이도 이해하기 쉬울 것입니다.

erase 연산은 스택 기반 방식과 재귀를 이용한 후위 순회 방식 모두 구현해 두었습니다.

from __future__ import annotations  
  
class Node:  
    def __init__(self):  
        self.__is_terminal: bool = False  
        self.__children: dict[str, Node] = {}  
  
    def mark_terminal(self) -> None:  
        self.__is_terminal = True  
  
    def release_terminal(self) -> None:  
        self.__is_terminal = False  
  
    def set_child(self, ch) -> None:  
        self.__children[ch] = Node()  
  
    def erase_child_hardly(self, ch) -> None:  
        del self.__children[ch]  
  
    def has_not_child(self, ch) -> bool:  
        return ch not in self.__children  
  
    def has_not_any_child(self) -> bool:  
        return not self.__children  
  
    def is_terminal(self) -> bool:  
        return self.__is_terminal  
  
    def is_not_terminal(self) -> bool:  
        return not self.is_terminal()  
  
    def get_child(self, ch) -> Node | None:  
        return self.__children.get(ch)  
  
  
class Trie:  
    def __init__(self):  
        self.__root = Node()  
  
    def insert(self, word) -> None:  
        curr = self.__root  
        for ch in word:  
            if curr.has_not_child(ch):  
                curr.set_child(ch)  
            curr = curr.get_child(ch)  
        curr.mark_terminal()  
  
    def search(self, word) -> bool:  
        curr = self.__root  
        for ch in word:  
            if curr.has_not_child(ch):  
                return False  
            curr = curr.get_child(ch)  
        return curr.is_terminal()  
  
    def erase(self, word) -> bool:  
        removal = []  
        curr = self.__root  
        for ch in word:  
            if curr.has_not_child(ch):  
                return False  
            removal.append([curr, ch])  
            curr = curr.get_child(ch)  
  
        curr.release_terminal()  
  
    def erase_recursive(self, word) -> bool:  
        w_depth = len(word)  
  
        def _erase(depth, curr) -> bool:  
            if depth == w_depth:  
                if not curr.is_terminal():  
                    raise KeyError("Word doesnt exist")  
                curr.release_terminal()  
                return curr.has_not_any_child()  
  
            ch = word[depth]  
            child = curr.get_child(ch)  
            if child is None:  
                raise KeyError("Word doesnt exist")  
            if _erase(depth + 1, child):  
                curr.erase_child_hardly(ch)  
            return curr.has_not_any_child() and curr.is_not_terminal()  
  
        return _erase(0, self.__root)  
  
    def starts_with(self, prefix) -> bool:  
        curr = self.__root  
        for ch in prefix:  
            if curr.has_not_child(ch):  
                return False  
            curr = curr.get_child(ch)  
        return True  
  
trie = Trie()  
trie.insert('string')  
trie.insert('stri')  
trie.insert('david')  
print(trie.search('string'), trie.search('stri'), trie.search('david'), sep='\n', end='\n\n')  
  
trie.erase('stri')  
print(trie.search('string'), trie.search('stri'), sep = '\n\n')  
  
print(trie.starts_with('str'))