Prefix sum
누적합(Prefix sum)은 배열의 시작점(보통 인덱스 0 또는 1)부터 특정 인덱스까지의 원소의 합을 말합니다. 예를 들어, 배열이 A = [a₀, a₁, ..., aₙ] 일 때, 인덱스 i 까지의 누적합 S[i] 는 다음과 같이 표현할 수 있습니다.
- Index 0 Base :
S[i] = a₀ + a₁ + ... + aᵢ - Index 1 Base :
S[i] = a₁ + a₂ + ... + aᵢ
누적합 배열을 미리 구해두면, 배열의 특정 구간합(Range sum)을 O(1)이라는 매우 빠른 시간 복잡도로 계산할 수 있습니다.
Prefix sum & Range sum
누적합과 구간합은 모두 배열이나 리스트의 원소들을 활용하여 합을 계산하는 기법이지만, 계산 방식과 목적이 다릅니다. 누적합은 각 인덱스까지의 합을 미리 계산하여 저장하는 반면, 구간합은 특정 구간의 합을 계산하는 데 사용됩니다. 즉, 누적합은 구간합을 계산하는 데 필요한 기반을 제공하며, 구간합은 누적합을 활용하여 특정 구간의 합을 빠르게 계산하는 데 사용됩니다.
1D Array Prefix sum
Index 1 Base
1차원 배열의 누적합 을 구할때는 주로 Index 1 Base 를 사용합니다. Index 1 Base 누적합 배열은 누적합 배열의 Index 0 은 비워두고 Index 1 부터 저장하는 방식입니다.
- 기존 arr 크기가 N 이라면, 누적합 배열의 크기는 (N + 1) 만큼 0 으로 초기화합니다.
psum = [0] * (N + 1) - arr 을 인덱스 1 ~ (N + 1) 까지 순회하며
psum[idx] = psum[idx - 1] + arr[idx - 1]를 진행합니다.

코드로는 다음과 같이 구현할 수 있습니다.
def solution(arr):
length = len(arr)
psum = [0] * (length + 1)
for idx in range(1, length + 1):
psum[idx] = psum[idx - 1] + arr[idx - 1]
return psum
print(solution([13, 19, 28, 23, 11, 25, 10, 20, 12, 24]))Index 0 Base
Index 0 Base 누적합 배열은 누적합 배열의 Index 0 부터 저장하는 방식입니다.
- 기존 arr 크기가 N 이라면, 누적합 배열의 크기도 N 만큼 0 으로 초기화합니다.
psum = [0] * N - 누적합 배열의 Index 0 을 arr[0] 값으로 초기화 시킵니다.
psum[0] = arr[0] - arr 을 인덱스 1 ~ N 까지 순회하며
psum[idx] = psum[idx - 1] + arr[idx]를 진행합니다.

코드로는 다음과 같이 구현할 수 있습니다.
def solution(arr):
length = len(arr)
psum = [0] * length
psum[0] = arr[0]
for idx in range(1, length):
psum[idx] = psum[idx - 1] + arr[idx]
return psum
print(solution([13, 19, 28, 23, 11, 25, 10, 20, 12, 24]))Index 0 Base 는 잘 사용 X
하지만 Index 0 Base 누적합 배열은 잘 사용하지 않습니다. 이는 이 누적합 배열을 이용하여 배열의 특정 구간의 구간합을 구할 때 시작 구간이 Index 0 이면, 인덱스 범위를 벗어나 예외가 발생하기 때문입니다. (파이썬에서는 -1 인덱스. 즉, 누적합 배열의 맨 뒤의 값을 참조하게 됩니다.) 따라서 시작 구간이 Index 0 을 포함한 구간의 합을 구할 때 예외처리 혹은 분기처리가 필요합니다.
해당 예외 케이스에 대한 부분은 Index 0 Base 엣지 케이스를 참고하면 됩니다.
Range sum
Index 1 Base
Index 1 Base 누적합 배열에서 연속된 구간 N ~ J 의 구간합을 구하고 싶다면 psum[J + 1] - psum[N] 를 해주면 됩니다. 아래 그림의 예시처럼 arr[3] ~ arr[5] 의 구간합을 구하려면 prefix_sum[6] - prefix_sum[3] 를 계산하면 됩니다.
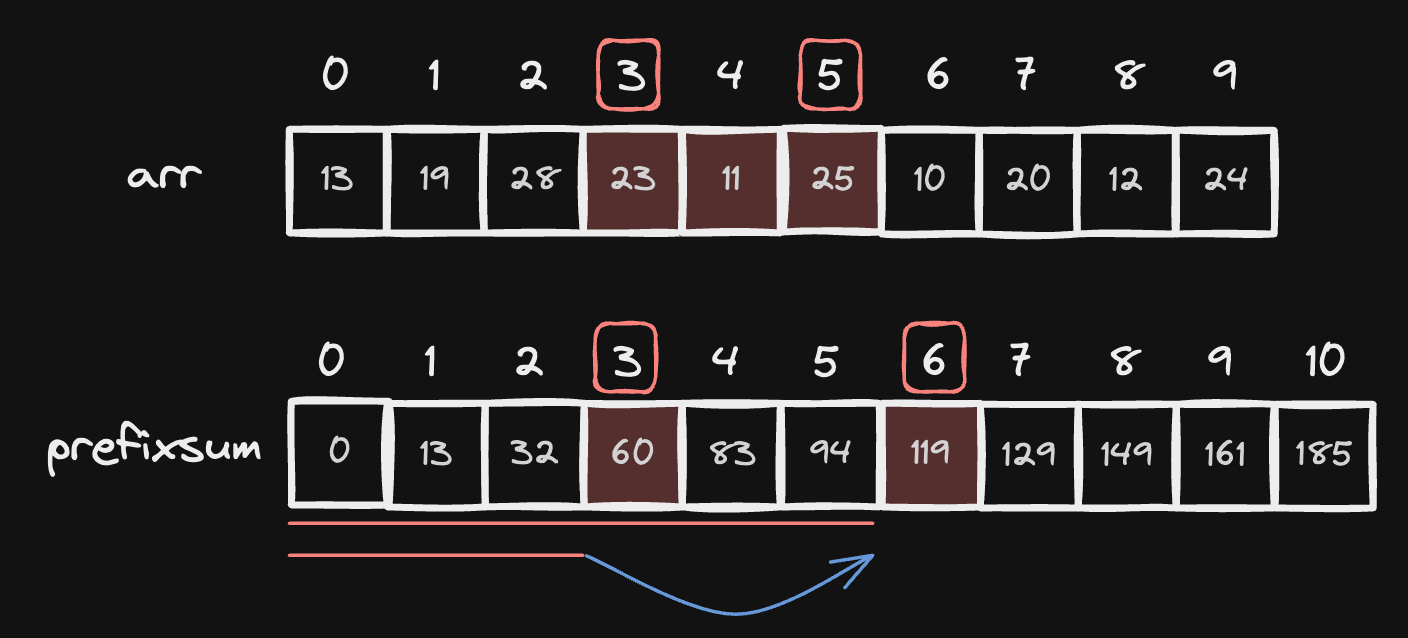
계산 과정은 아래 그림을 보면 이해할 수 있을것입니다.

코드로는 다음과 같이 구현할 수 있습니다. 누적합 배열 psum 만 구해놓으면 딱히 할게 없습니다.
def solution(arr, prolog, epilog):
length = len(arr)
psum = [0] * (length + 1)
for idx in range(1, length + 1):
psum[idx] = psum[idx - 1] + arr[idx - 1]
return psum[epilog + 1] - psum[prolog]
print(solution([13, 19, 28, 23, 11, 25, 10, 20, 12, 24], 3, 5))Index 0 Base 엣지 케이스
Index 0 Base 누적합 배열에서 연속된 구간 N ~ J 의 구간합을 구하고 싶다면 psum[J] - psum[N - 1] 를 해주면 됩니다. 아래 예시처럼 arr[3] ~ arr[5] 의 구간합을 구하려면 psum[5] - psum[2] 를 계산하면 됩니다.
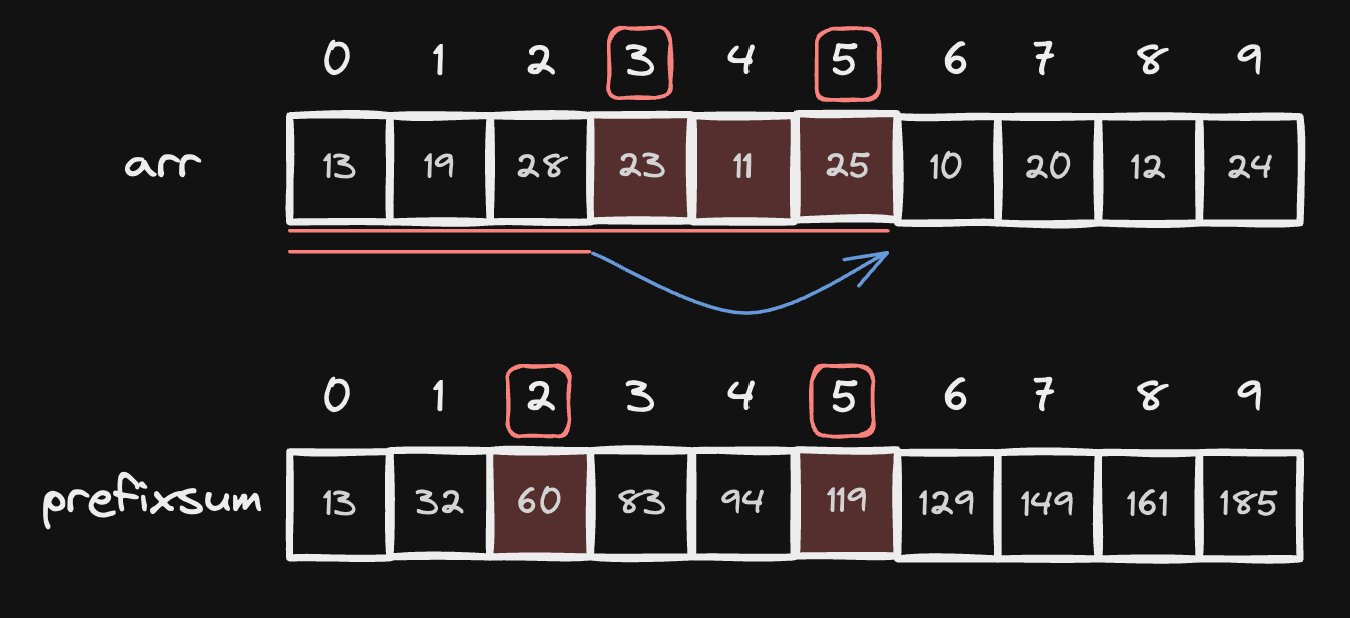
계산 과정은 아래 그림을 보면 이해할 수 있습니다.

코드로는 다음과 같이 구현할 수 있습니다. 마찬가지로 psum 만 구해놓으면 딱히 할게 없습니다.
def solution(arr, prolog, epilog):
length = len(arr)
psum = [0] * length
psum[0] = arr[0]
for idx in range(1, length):
psum[idx] = psum[idx - 1] + arr[idx]
return psum[epilog] - psum[prolog - 1]
print(solution([13, 19, 28, 23, 11, 25, 10, 20, 12, 24], 3, 5))앞서 Index 0 Base 누적합 배열은 잘 사용하지 않는다고 언급하였습니다. arr 배열의 0 ~ 3 의 구간합을 구하는 경우를 봐보겠습니다.
- arr 0 ~ 3 의 구간합을 구하려면
psum[3] - psum[0 - 1]을 수행하면 됩니다. - 하지만
psum[0 - 1]는psum[-1]. 즉, 파이썬에서 psum 배열의 맨 마지막 원소를 말하기 때문에 arr 배열의 원소를 모두 더한 값을 참조하게 되어 이상한 값이 출력되게 됩니다.
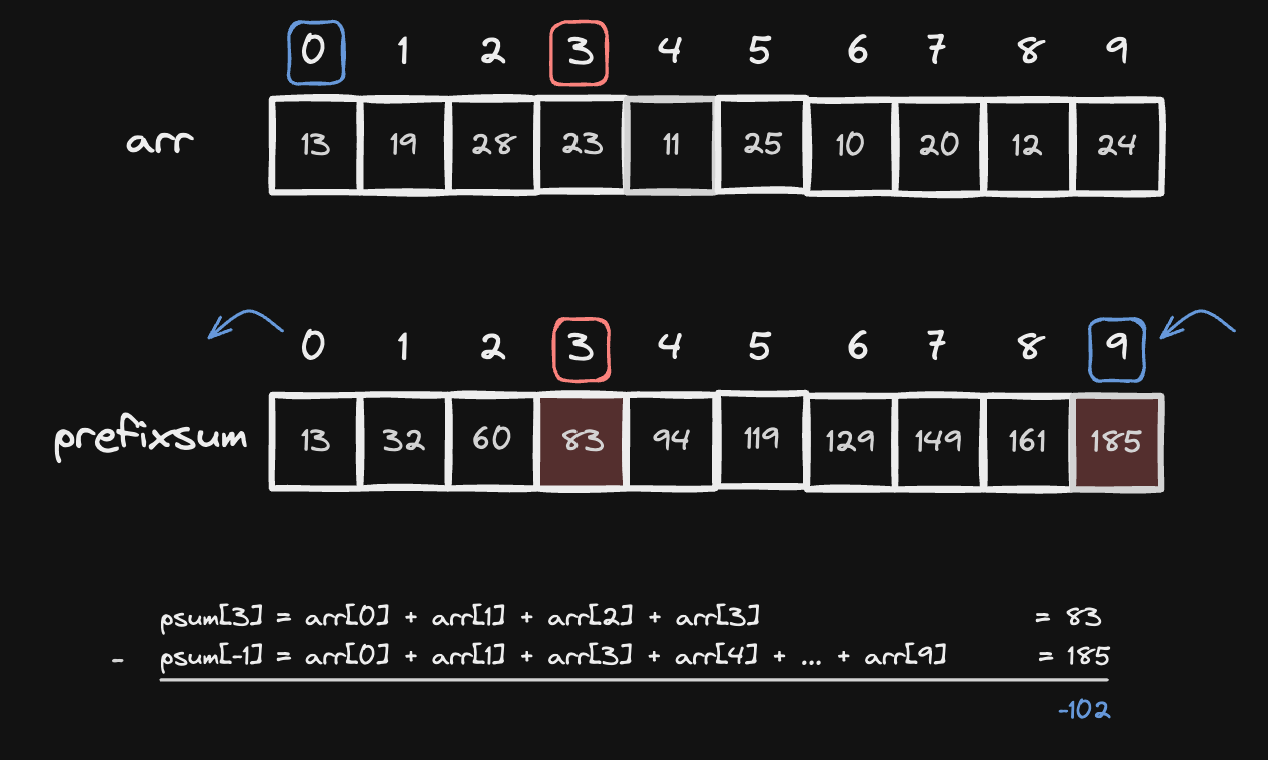
이를 해결하기 위해 추가적인 예외처리 혹은 분기처리가 들어가기 때문에 효율적이지 않습니다.
def solution(arr, prolog, epilog):
length = len(arr)
psum = [0] * length
psum[0] = arr[0]
for idx in range(1, length):
psum[idx] = psum[idx - 1] + arr[idx]
if prolog == 0:
return psum[epilog]
return psum[epilog] - psum[prolog - 1]
print(solution([13, 19, 28, 23, 11, 25, 10, 20, 12, 24], 0, 3))2D Prefix sum
2차원 배열의 누적합은 1차원보다 조금 더 복잡합니다. 우선 2차원 배열 arr에 대한 누적합을 저장할 2차원 배열 psum이 필요합니다.
- 만약
arr의 크기가N x M이라면, 누적합 배열psum의 크기는(N + 1) x (M + 1)로 생성합니다. - 이렇게
+1씩 늘리는 이유는인덱스 경계 처리를 간단하게 하기 위해서입니다. 0행과 0열은 모두 0으로 초기화해두고, 계산 시 자연스럽게 누적이 가능하도록 합니다.
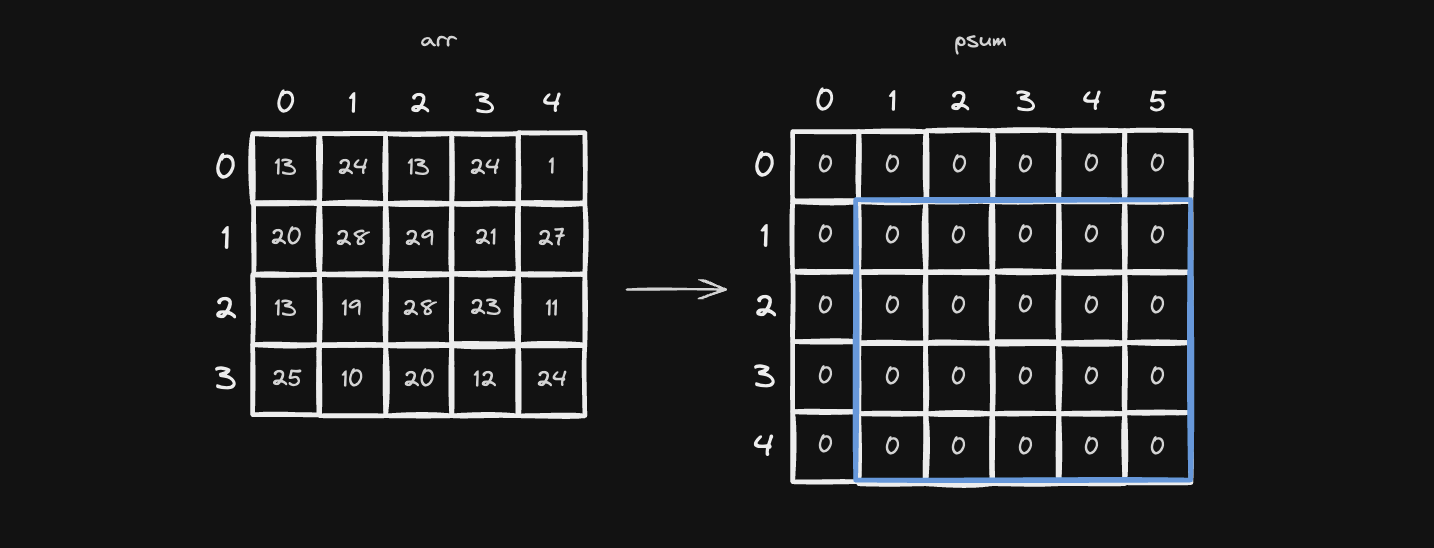
2차원 배열의 누적합은 (1 ~ N) x (1 ~ M) 범위에서 이중 반복문을 통해 구합니다. 현재 좌표가 (row, col)일 때 psum[row][col]은 arr[row - 1][col - 1]까지의 누적합을 의미하며, 아래 공식을 따릅니다.
psum[row][col] = psum[row - 1][col] + psum[row][col - 1]
- psum[row - 1][col - 1]
+ arr[row - 1][col - 1]결과적으로, arr 의 각 좌표에 대한 누적합은 아래와 같이 나오게 됩니다.

이해를 위해 psum[4][3] 예시를 보겠습니다.
psum[4][3]은arr[3][2]까지의 전체 누적합을 의미합니다.psum[4][3] = psum[3][3] + psum[4][2] - psum[3][2] + arr[3][2]입니다.- 바로 위 수식은 아래 그림에서 순서대로
파랑 = 빨강 + 초록 - 갈색 + arr[3][2]에 해당합니다. - 빨강과 초록을 더하면 갈색 영역(중복 영역)이 두 번 더해지므로 한 번 빼주고, 마지막에 현재 위치인
arr[3][2]값을 더해주는 원리입니다.
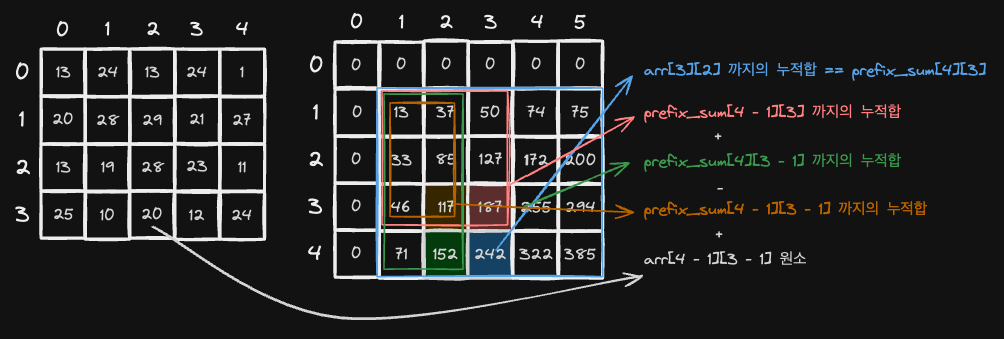
더 풀어서 그려볼 수 있습니다. psum[3][3] 과 psum[4][2] 을 더하면 psum[3][2] 부분이 한번 더 더해지기 때문에 갈색 부분을 한번 빼주는 것입니다. 이제 원본 배열의 arr[3][2] 값을 더해주면, psum[4][3], 즉 arr[3][2]까지의 누적합이 완성됩니다.


코드로는 다음과 같이 구현할 수 있습니다.
def solution(arr):
N, M = len(arr), len(arr[0])
psum = [[0] * (M + 1) for _ in range(N + 1)]
for row in range(1, N + 1):
for col in range(1, M + 1):
psum[row][col] = psum[row - 1][col] + psum[row][col - 1] \
- psum[row - 1][col - 1] \
+ arr[row - 1][col - 1]
return psum
print(
solution(
[
[13, 24, 13, 24, 1],
[20, 28, 29, 21, 27],
[13, 19, 28, 23, 11],
[25, 10, 20, 12, 24]
]
)
)Range sum
2차원 배열에서 구간합을 구하려면 앞서 구한 누적합 배열을 이용하면 됩니다. 구간합은 아래 공식을 따릅니다.
# 만약, arr[r1][c1] ~ arr[r2][c2] 까지의 구간합을 구한다면
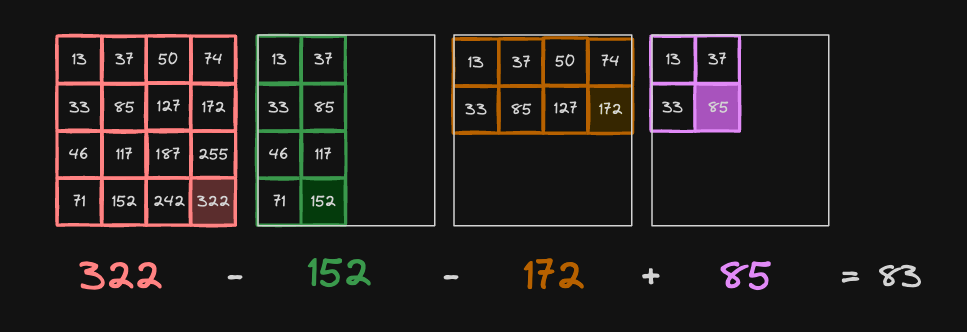
psum[r2 + 1][c2 + 1] - psum[r1][c2 + 1] - psum[r2 + 1][c1] + psum[r1][c1]예로 arr[2][2] ~ arr[3][3] 까지의 구한다면, 다음 공식을 수행하면 됩니다.
psum[4][4] - psum[2][4] - psum[4][2] + psum[2][2]
누적합을 구할때와 비슷하게, 초록색부분과 갈색부분을 빼주면 보라색부분이 한번 더 빼지기 때문에, 이를 보충하기 위해 보라색 부분을 한번 더해줍니다.
코드로는 다음과 같이 구현할 수 있습니다.
def solution(arr, prolog, epilog):
N, M = len(arr), len(arr[0])
psum = [[0] * (M + 1) for _ in range(N + 1)]
for row in range(1, N + 1):
for col in range(1, M + 1):
psum[row][col] = psum[row - 1][col] + psum[row][col - 1] \
- psum[row - 1][col - 1] \
+ arr[row - 1][col - 1]
r1, c1 = prolog
r2, c2 = epilog
return psum[r2 + 1][c2 + 1] - psum[r1][c2 + 1] - psum[r2 + 1][c1] + psum[r1][c1]
print(
solution(
[
[13, 24, 13, 24, 1],
[20, 28, 29, 21, 27],
[13, 19, 28, 23, 11],
[25, 10, 20, 12, 24]
],
(2, 2),
(3, 3)
)
)